Plugin WindLab: Difference between revisions
| (16 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
|Version=1.0 | |Version=1.0 | ||
|Date=2024-04-15 | |Date=2024-04-15 | ||
|Features= | |Features= [[#Horizontal_Uniform_Distribution|Horizontal Uniform Distribution]], [[#Vertical_Uniform_Distribution|Vertical Uniform Distribution]], [[#Uniform_Distribution|Uniform Distribution]], [[#Grid_Points|Grid Points]], [[#General_Distribution|General Distribution]], [[#Import_Simulation_Points_from_File|Import Simulation Points from File]], [[#Power_Law_Profile|Power Law Profile]], [[#Logarithmic_Law_Profile|Logarithmic Law Profile]], [[#Deaves_and_Harris_Profile|Deaves and Harris Profile]], [[#Sine_Modulation_Function|Sine Modulation Function]], [[#Three_Parameter_Modulation_Function|Three Parameter Modulation Function]], [[#Exponential_Modulation_Function|Exponential Modulation Function]], [[#Davenport_Coherence_Function|Davenport Coherence Function]], [[#Krenk_Coherence_Function|Krenk Coherence Function]], [[#Davenport_Along_Wind_Spectrum|Davenport Along Wind Spectrum]], [[#Harris_Along_Wind_Spectrum|Harris Along Wind Spectrum]], [[#Kaimal_Along_Wind_Spectrum|Kaimal Along Wind Spectrum]], [[#Kaimal_Across_Wind_Spectrum|Kaimal Across Wind Spectrum]], [[#Kaimal_Vertical_Wind_Spectrum|Kaimal Vertical Wind Spectrum]], [[#Simiu_Along_Wind_Spectrum|Simiu Along Wind Spectrum]], [[#Simiu_Across_Wind_Spectrum|Simiu Across Wind Spectrum]], [[#Simiu_Vertical_Wind_Spectrum|Simiu Vertical Wind Spectrum]], [[#von_Karman_Along_Wind_Spectrum|von Karman Along Wind Spectrum]], [[#Uniform_Random_Phases|Uniform Random Phases]], [[#Uniform_Random_Phases_Import|Uniform Random Phases Import]], [[#Double_Index_Frequency_Discretization|Double Index Frequency Discretization]], [[#Single_Index_Frequency_Discretization|Single Index Frequency Discretization]], [[#Zerva_Frequency_Discretization|Zerva Frequency Discretization]], [[#George_Deodatis_Simulation_Method_1996|George Deodatis Simulation Method(1996)]], [[#Cholesky_Decomposition|Cholesky Decomposition]] | ||
| Line 12: | Line 12: | ||
You can find the source code of this plugin on the following Github repository: [https://github.com/LabRPS/LabRPS-plugins/tree/master/WindLab/WindLabPlugin Get the code here!]. This plugin is one of the official plugins provided by LabRPS. It provides very useful features (tools) for the simulation of random wind velocity. Plugins are very easy to create in LabRPS, therefore, anyone can develop plugin for any random phenomenon in LabRPS. Go to this [[Plugin_Creation|page]] to see how to create new plugin for LabRPS. You can get quick assistance from LabRPS community by sending your concern to the [https://labrps.com/boards community forum]. | You can find the source code of this plugin on the following Github repository: [https://github.com/LabRPS/LabRPS-plugins/tree/master/WindLab/WindLabPlugin Get the code here!]. This plugin is one of the official plugins provided by LabRPS. It provides very useful features (tools) for the simulation of random wind velocity. Plugins are very easy to create in LabRPS, therefore, anyone can develop plugin for any random phenomenon in LabRPS. Go to this [[Plugin_Creation|page]] to see how to create new plugin for LabRPS. You can get quick assistance from LabRPS community by sending your concern to the [https://labrps.com/boards community forum]. | ||
== | == Horizontal Uniform Distribution == | ||
This feature | This feature provides an efficient method to distribute random wind simulation points uniformly in space. It allows users to generate a set of points within a 3D spatial domain, ensuring that the points are evenly distributed along a horizontal line that is parallel to one of the coordinate system axis. This uniform distribution is critical in certain simulation methods. For <math>n</math> simulation points <math>(P_1,P_2,P_3,...,P_n)</math>, the distance <math>d_{jk}</math> between points <math>P_j</math> and <math>P_k</math> must be given by the following formula: | ||
<math | <math>d_{jk} = s\times|j-k|</math> | ||
where <math>s</math> is the even space between any two adjacent points. | |||
=== Properties === | |||
* {{PropertyData|FirstPoint}}: This is a point in 3D space representing the first point the distribution will start from. | |||
* {{PropertyData|Spacing}}: This is the even space between any two adjacent points in the distribution. | |||
=== Scripting === | === Scripting === | ||
{{Code|code= | {{Code|code= | ||
| Line 40: | Line 33: | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import numpy | import numpy | ||
import LabRPS | |||
def compute(): | def compute(): | ||
installResuslt = WindLab.installPlugin("WindLabPlugin") | installResuslt = WindLab.installPlugin("WindLabPlugin") | ||
doc = | doc = LabRPS.ActiveDocument | ||
if not doc: | if not doc: | ||
doc = | doc = LabRPS.newDocument() | ||
# create WindLab simulation called "Simulation" | # create WindLab simulation called "Simulation" | ||
| Line 56: | Line 50: | ||
return None | return None | ||
featureType = " | featureType = "Horizontal Distribution" | ||
featureGroup = " | featureGroup = "Location Distribution" | ||
# create the feature | # create the feature | ||
newFeature= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not newFeature: | ||
LabRPS.Console.PrintError("Error on creating the | LabRPS.Console.PrintError("Error on creating the feature.\n") | ||
return None | return None | ||
# | # let's set the first point of the distribution (x =0, y = 0, z = 80m) | ||
newFeature.FirstPoint = vec(0,0,80000) | |||
# let's set the spacing (s = 10m) | |||
newFeature.Spacing = '10m' | |||
# compute the simulation points coordinates. WindLab will internally use the "newFeature" feature. | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | simPoints = sim.computeLocationCoordinateMatrixP3() | ||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | |||
arr = numpy.asarray(simPoints) | |||
# | # you can also show the result in a table, pass False as last argument to the function to ask | ||
# LabRPS to only show the data without plotting them | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False) | |||
compute() | |||
compute() | |||
}} | }} | ||
[[#top| Back to the Top ]] | |||
== | == Vertical Uniform Distribution == | ||
This feature provides an efficient method to distribute random wind simulation points uniformly in space. It allows users to generate a set of points within a 3D spatial domain, ensuring that the points are evenly distributed along a | This feature provides an efficient method to distribute random wind simulation points uniformly in space. It allows users to generate a set of points within a 3D spatial domain, ensuring that the points are evenly distributed along a vertical line. This uniform distribution is critical in certain simulation methods. For <math>n</math> simulation points <math>(P_1,P_2,P_3,...,P_n)</math>, the distance <math>d_{jk}</math> between points <math>P_j</math> and <math>P_k</math> must be given by the following formula: | ||
<math>d_{jk} = s\times|j-k|</math> | <math>d_{jk} = s\times|j-k|</math> | ||
| Line 107: | Line 92: | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|LowestPoint}}: This is a point in 3D space representing the lowest point the distribution will start from. In many applications, this point should not be lower than 10 meters. | ||
* {{PropertyData|Spacing}}: This is the even space between any two adjacent points in the distribution. | * {{PropertyData|Spacing}}: This is the even space between any two adjacent points in the distribution. | ||
| Line 118: | Line 103: | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import numpy | import numpy | ||
import LabRPS | |||
def compute(): | def compute(): | ||
installResuslt = WindLab.installPlugin("WindLabPlugin") | installResuslt = WindLab.installPlugin("WindLabPlugin") | ||
doc = | doc = LabRPS.ActiveDocument | ||
if not doc: | if not doc: | ||
doc = | doc = LabRPS.newDocument() | ||
# create WindLab simulation called "Simulation" | # create WindLab simulation called "Simulation" | ||
| Line 134: | Line 120: | ||
return None | return None | ||
featureType = " | featureType = "Vertical Distribution" | ||
featureGroup = "Location Distribution" | featureGroup = "Location Distribution" | ||
| Line 145: | Line 131: | ||
return None | return None | ||
# let's set the first point of the distribution (x =0, y = 0, z = | # let's set the first point of the distribution (x =0, y = 0, z = 30m) | ||
newFeature. | newFeature.LowestPoint = vec(0,0,30000) | ||
# let's set the spacing (s = 10m) | # let's set the spacing (s = 10m) | ||
newFeature.Spacing = '10m' | newFeature.Spacing = '10m' | ||
# compute the simulation points coordinates. WindLab will internally use the " | # compute the simulation points coordinates. WindLab will internally use the "newFeature" feature. | ||
simPoints = sim.computeLocationCoordinateMatrixP3() | simPoints = sim.computeLocationCoordinateMatrixP3() | ||
| Line 166: | Line 152: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Uniform Distribution == | ||
This feature | This feature may be seen as a general form of the horizontal and the vertical distribution features. It allows users to generate a set of points within a 3D spatial domain, ensuring that the points are evenly distributed along a line parallel to one of the coordinate system axis. For <math>n</math> simulation points <math>(P_1,P_2,P_3,...,P_n)</math>, the distance <math>d_{jk}</math> between points <math>P_j</math> and <math>P_k</math> must be given by the following formula: | ||
<math>d_{jk} = s\times|j-k|</math> | <math>d_{jk} = s\times|j-k|</math> | ||
| Line 176: | Line 162: | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|FirstPoint}}: This is a point in 3D space representing the first point the distribution will start from. This should be the lowest point in case the distribution is parallel to the vertical axis and should not be lower than 10 meters in many application. | ||
* {{PropertyData|Spacing}}: This is the even space between any two adjacent points in the distribution. | * {{PropertyData|Spacing}}: This is the even space between any two adjacent points in the distribution. | ||
* {{PropertyData|Direction}}: Its value can be X, Y or Z. This is the axis the points distribution is parallel to. | |||
=== Scripting === | === Scripting === | ||
This feature can be used to produce vertical distribution as we did before in the Vertical Distribution feature. | |||
{{Code|code= | {{Code|code= | ||
| Line 187: | Line 176: | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import numpy | import numpy | ||
import LabRPS | |||
def compute(): | def compute(): | ||
installResuslt = WindLab.installPlugin("WindLabPlugin") | installResuslt = WindLab.installPlugin("WindLabPlugin") | ||
doc = | doc = LabRPS.ActiveDocument | ||
if not doc: | if not doc: | ||
doc = | doc = LabRPS.newDocument() | ||
# create WindLab simulation called "Simulation" | # create WindLab simulation called "Simulation" | ||
sim = WindLabObjects.makeSimulation(doc, "Simulation") | sim = WindLabObjects.makeSimulation(doc, "Simulation") | ||
# check if the simulation | # check if the simulation does really exist | ||
if not sim: | if not sim: | ||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = " | featureType = "Uniform Distribution" | ||
featureGroup = "Location Distribution" | featureGroup = "Location Distribution" | ||
# create the feature | # create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in | ||
# case you don't understand the next line) | |||
unifSimPoints= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not unifSimPoints: | ||
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n") | |||
# abord the computation | |||
# set the direction of the distribution to be vertical | |||
unifSimPoints.Direction= 'Z' | |||
# let's set the first point of the distribution (x =0, y = 0, z = 30m) | # let's set the first point of the distribution (x =0, y = 0, z = 30m) | ||
unifSimPoints.FirstPoint = vec(0,0,30000) # This is the lowest point in this case (Direction = 'Z') | |||
# let's set the spacing (s = 10m) | # let's set the spacing (s = 10m) | ||
unifSimPoints.Spacing = '10m' | |||
# compute the simulation points coordinates. WindLab will internally use the " | # compute the simulation points coordinates. WindLab will internally use the "unifSimPoints" feature. | ||
simPoints = sim.computeLocationCoordinateMatrixP3() | simPoints = sim.computeLocationCoordinateMatrixP3() | ||
| Line 233: | Line 227: | ||
}} | }} | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Grid Points == | ||
This feature | This feature allows users to generate a set of grid points within a 3D spatial domain, ensuring that the points are evenly distributed in a plane parallel to one of the coordinate system planes (XY Plane, YZ Plane, XZ Plane). | ||
=== Properties === | |||
* {{PropertyData|Spacing1}}: This is the points spacing along one of the axis forming the plane. | |||
* {{PropertyData|Spacing2}}: This is the points spacing along the second axis. | |||
* {{PropertyData|Length1}}: This is the length within points are distributed along one of the axis forming the plane. | |||
* {{PropertyData|Length2}}: This is the length within points are distributed along the second axis. | |||
* {{PropertyData| | * {{PropertyData|CenterPoint}}: This is the center of the grid around which the points are generated. It is a 3D point. | ||
* {{PropertyData| | * {{PropertyData|NumberOfPoints}}: This is the resulting total number of points in the grid. This is a read only property for internal use. User cannot change its value directly. | ||
* {{PropertyData| | |||
=== Scripting === | === Scripting === | ||
The following script shows how this feature can be created and used. | |||
{{Code|code= | {{Code|code= | ||
import WindLab | import WindLab | ||
import GeneralToolsGui | |||
import WindLabObjects | import WindLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import LabRPS | |||
import numpy | import numpy | ||
import matplotlib.pyplot as plt | |||
from mpl_toolkits.mplot3d import Axes3D | |||
def compute(): | |||
# get an existing WindLab simulation called "Simulation" | |||
sim = WindLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = "Grid Points" | |||
featureGroup = "Location Distribution" | |||
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in | |||
# case you don't understand the next line) | |||
unifSimPoints= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not unifSimPoints: | |||
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n") | |||
# abord the computation | |||
# set the plan the points grid is parallel to | |||
unifSimPoints.LocationPlan= 'YZ Plane' | |||
# let's set the center point of the distribution (x =0, y = 0, z = 0) | |||
unifSimPoints.CenterPoint = vec(0,0,0) | |||
# let's set the spacing1 (s1 = 10m) | |||
unifSimPoints.Spacing1 = '10m' | |||
# let's set the spacing2 (s2 = 10m) | |||
unifSimPoints.Spacing2 = '10m' | |||
# let's set the length1 (l1 = 200m) | |||
unifSimPoints.Length1= '200m' | |||
# let's set the length2 (l2 = 200m) | |||
unifSimPoints.Length2= '200m' | |||
# compute the simulation points coordinates. WindLab will internally use the "unifSimPoints" feature. | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
= | # now you can convert the coordinate matrix to numpy array and use it for any other purposes | ||
arr = numpy.asarray(simPoints) | |||
# Example 3D points | |||
x = arr[:,1] | |||
y = arr[:,2] | |||
z = arr[:,3] | |||
# you can also show the result in a table, pass False as last argument to the function to ask | |||
# LabRPS to only show the data without plotting them | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False) | |||
# Create a figure | |||
fig = plt.figure() | |||
== | # Add 3D axes | ||
ax = fig.add_subplot(111, projection='3d') | |||
# Plot points | |||
ax.scatter(x, y, z, color='blue') | |||
# Hide all axes and labels | |||
ax.set_axis_off() | |||
# Set the title | |||
ax.set_title('3D Plotting of Points') | |||
# Show the plot | |||
plt.show() | |||
compute() | |||
}} | }} | ||
| Line 384: | Line 350: | ||
{{Code|code= | {{Code|code= | ||
import WindLab | import WindLab | ||
import GeneralToolsGui | |||
import WindLabObjects | import WindLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import LabRPS | |||
import numpy | import numpy | ||
def compute(): | |||
installResuslt = WindLab.installPlugin("WindLabPlugin") | |||
doc = LabRPS.ActiveDocument | |||
if not doc: | |||
doc = LabRPS.newDocument() | |||
# create WindLab simulation called "Simulation" | |||
sim = WindLabObjects.makeSimulation(doc, "Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = "General Distribution" | |||
featureGroup = "Location Distribution" | |||
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in | |||
# case you don't understand the next line) | |||
genSimPoints= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not genSimPoints: | |||
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n") | |||
# abord the computation | |||
# create the simulation points by their coordinates | |||
v1 = vec(0, 0, 35000) | |||
v2 = vec(0, 0, 40000) | |||
v3 = vec(0, 0, 140000) | |||
# add the points to the locations | |||
genSimPoints.Locations = [v1, v2, v3] | |||
# compute the simulation points coordinates. WindLab will internally use the "genSimPoints" feature | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | |||
arr = numpy.asarray(simPoints) | |||
# you can also show the result in a table, pass False as last argument to the function to ask | |||
# LabRPS to only show the data without plotting them | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False) | |||
compute() | |||
}} | }} | ||
| Line 441: | Line 422: | ||
{{Code|code= | {{Code|code= | ||
import WindLab | import WindLab | ||
import GeneralToolsGui | |||
import WindLabObjects | import WindLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import LabRPS | |||
import numpy | import numpy | ||
def compute(): | |||
installResuslt = WindLab.installPlugin("WindLabPlugin") | |||
doc = LabRPS.ActiveDocument | |||
if not doc: | |||
doc = LabRPS.newDocument() | |||
# create WindLab simulation called "Simulation" | |||
sim = WindLabObjects.makeSimulation(doc, "Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = "Import Simulation Points from File" | |||
featureGroup = "Location Distribution" | |||
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in | |||
# case you don't understand the next line) | |||
simPoints= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not simPoints: | |||
LabRPS.Console.PrintError("Error on creating the simulation points feature.\n") | |||
# abord the computation | |||
# set the direction of the distribution to be vertical | |||
simPoints.FilePath = "D:/Points.txt" | |||
# compute the simulation points coordinates. WindLab will internally use the "simPoints" feature. | |||
importedSimPoints = sim.computeLocationCoordinateMatrixP3() | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | |||
arr = numpy.asarray(importedSimPoints ) | |||
# you can also show the result in a table, pass False as last argument to the function to ask | |||
# LabRPS to only show the data without plotting them | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, importedSimPoints, False) | |||
compute() | |||
}} | }} | ||
| Line 504: | Line 500: | ||
{{Code|code= | {{Code|code= | ||
import WindLab | import WindLab | ||
import GeneralToolsGui | |||
import WindLabObjects | import WindLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import LabRPS | |||
import numpy | import numpy | ||
def compute(): | |||
installResuslt = WindLab.installPlugin("WindLabPlugin") | |||
# get an existing WindLab simulation called "Simulation" | |||
sim = WindLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = "Power Law Profile" | |||
featureGroup = "Mean Wind Profile" | |||
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in | |||
# case you don't understand the next line) | |||
meanSpeed= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not meanSpeed: | |||
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n") | |||
# abord the computation | |||
meanSpeed.ReferenceHeight = '10.00 m' | |||
meanSpeed.ReferenceSpeed = '30.00 m/s' | |||
meanSpeed.DimensionlessPower = 0.12 | |||
meanSpeed.ZeroPlanDisplacement = '0.0 m' | |||
# In WindLab, mean wind velocity can vary with time. In case the user desires a time dependent mean wind speed, | |||
# a modulation function can be used for this purpose. The feature account for this. When the Stationarity property of the parent | |||
# simulation of this feature is false, the feature identify the active modulation function and use it to produce non-stationary | |||
# mean wind speed. But for this example we shall use time instant of 0 second. | |||
time = 0.0 | |||
# compute the mean wind speeds at time instant of 0 second and for all simulation points | |||
# Note that when the following code is run, WindLab will try to identify the active locations distribution, | |||
# it will also try to identity the active modulation function in case the parent simulation is non-stationary. | |||
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
meanValues = sim.computeMeanWindSpeedVectorP(time) | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | |||
arr = numpy.asarray(meanValues ) | |||
# you can also show the result in a table, pass False as last argument to the function to ask | |||
# LabRPS to only show the data without plotting them | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 2, meanValues, False) | |||
compute() | |||
}} | }} | ||
| Line 1,903: | Line 1,910: | ||
arr = numpy.asarray(frequencyMatrix) | arr = numpy.asarray(frequencyMatrix) | ||
}} | |||
[[#top| Back to the Top ]] | |||
== George Deodatis Simulation Method 1996 == | |||
The paper "Simulation of Ergodic Multivariate Stochastic Processes" by G. Deodatis (1996) presents a method for simulating multivariate stochastic processes, particularly focusing on ergodic processes. The goal of the paper is to provide an efficient method to simulate multivariate stochastic processes that are ergodic. Ergodic processes are those where time averages of the process can be taken as realizations of the ensemble averages. The method is applicable to a wide range of stochastic processes, particularly those in engineering and environmental sciences (e.g., wind, seismic activity, or oceanography). | |||
According to the method, the stochastic process <math>f_{j}(t) (j = 1, 2, 3, ..., n)</math> can be simulated by the following series as: | |||
<math>f_{j}(t) = 2\sum_{m=1}^{n}\sum_{l=1}^{N}|H_{jm}(\omega_{ml})|\sqrt{\Delta\omega}\cos\left[\omega_{ml}t+\theta_{jm}(\omega_{ml})+\Phi_{ml}\right];\quad j = 1, 2, 3, ..., n;\quad l = 1, 2, 3, ..., N</math> | |||
where: | |||
* <math>S(\omega) = H(\omega)H^{T*}(\omega)</math>, | |||
* <math>\theta_{jm}(\omega_{ml}) = tan^{-1}\left(\frac{Im[H_{jm}(\omega_{ml})]}{Re[H_{jm}(\omega_{ml})]}\right)</math>, | |||
* <math>f_{j}(t)</math> is the wind velocity at time instant <math>t</math> and location <math>j</math>, | |||
* <math>\Delta\omega</math> is the frequency increment, | |||
* <math>N</math> is the number of frequency increments, | |||
* <math>\Phi_{ml}</math> are <math>n</math> sequences of independent random phase angles distributed uniformly over the interval <math>\left [ 0,2\pi \right ]</math>. | |||
Refer to the paper for more details. Not that, in LabRPS this feature depends on some other features such as location distribution, mean wind profile, power spectral density, coherence function among others. These dependent features must me be created first. You can run the feature any time and follow the error messages to identify the missing feature that you need to create. You can also refer to the script below to identify all required features. In case you want to obtain the results as presented in the paper, you need to used all the parameters as presented in the paper. | |||
=== Scripting === | |||
The following script shows how this feature can be created and used. | |||
{{Code|code= | |||
import LabRPS | |||
import WindLab | |||
import WindLabObjects | |||
from LabRPS import Vector as vec | |||
import time | |||
def simulate(): | |||
# Plugin | |||
installResuslt = WindLab.installPlugin("WindLabPlugin") | |||
if not installResuslt: | |||
LabRPS.Console.PrintError("The installation the WindLabPlugin has failed.\n") | |||
return None | |||
# Document | |||
doc = LabRPS.newDocument() | |||
# Simulation | |||
sim = WindLabObjects.makeSimulation(doc, "Simulation") | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
# set simulation parameters | |||
sim.NumberOfFrequency = 2048 | |||
sim.MaxFrequency = "0.64 Hz" # 4 rad/s; | |||
sim.FrequencyIncrement = "0.00031 Hz" # 0.00195 rad/s; | |||
sim.TimeIncrement = "0.785 s" | |||
sim.NumberOfTimeIncrements = 9651 | |||
# Simulation points | |||
loc = WindLabObjects.makeFeature("SimulationPoints", "Simulation", "General Distribution", "Location Distribution") | |||
if not loc: | |||
LabRPS.Console.PrintError("Error on creating the location distribution.\n") | |||
return None | |||
v1 = vec(0, 0, 35) | |||
v2 = vec(0, 0, 40) | |||
v3 = vec(0, 0, 140) | |||
loc.Locations = [v1, v2, v3] | |||
# Mean wind Profile | |||
mean = WindLabObjects.makeFeature("MeanSpeed", "Simulation", "Logarithmic Law Profile", "Mean Wind Profile") | |||
if not mean: | |||
LabRPS.Console.PrintError("The creation of the mean wind profile was not successuful.\n") | |||
return None | |||
mean.TerrainRoughness = '0.001266 m' | |||
mean.ShearVelocity = '1.76 m/s' | |||
# Frequencies | |||
frequency = WindLabObjects.makeFeature("Frequencies", "Simulation", "Double Index Frequency Discretization", "Frequency Distribution") | |||
if not frequency: | |||
LabRPS.Console.PrintError("Error on creating the frequency distribution.\n") | |||
return None | |||
# Spectrum | |||
spectrum = WindLabObjects.makeFeature("Spectrum", "Simulation", "Kaimal Along Wind Spectrum", "Along Wind Spectrum") | |||
if not spectrum: | |||
LabRPS.Console.PrintError("Error on creating the spectrum model.\n") | |||
return None | |||
# Coherence | |||
coherence = WindLabObjects.makeFeature("CoherenceFunction", "Simulation", "Davenport Coherence Function", "Coherence Function") | |||
if not coherence: | |||
LabRPS.Console.PrintError("The creation of the coherence was not successuful.\n") | |||
return None | |||
coherence.ExponentialDecayCz = 10 | |||
# Spectrum decomposition | |||
spectrumD = WindLabObjects.makeFeature("SpectrumDecomposition", "Simulation", "Cholesky Decomposition", "Spectrum Decomposition Method") | |||
if not spectrumD: | |||
LabRPS.Console.PrintError("Error on creating the spectrum decomposition method.\n") | |||
return None | |||
# Random phase | |||
randomness = WindLabObjects.makeFeature("RandomPhases", "Simulation", "Uniform Random Phases", "Randomness Provider") | |||
if not randomness: | |||
LabRPS.Console.PrintError("The creation of the randomness provider was not successuful.\n") | |||
return None | |||
# Simulation method | |||
simMethod = WindLabObjects.makeFeature("SimulationMethod", "Simulation", "Deodatis 1996", "Simulation Method") | |||
if not simMethod: | |||
LabRPS.Console.PrintError("Error on creating the simulation method.\n") | |||
return None | |||
# Run simulation and output the first(0) sample | |||
# store starting time | |||
begin = time.time() | |||
velocities = sim.simulate(0) | |||
# store end time | |||
end = time.time() | |||
LabRPS.Console.PrintMessage(f"Total runtime of the simulaltion is {end - begin} seconds\n") | |||
if LabRPS.GuiUp: | |||
import WindLabGui | |||
import GeneralToolsGui | |||
WindLabGui.setActiveSimulation(sim) | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfTimeIncrements, sim.getSimulationData().numberOfSpatialPosition + 1, velocities, True) | |||
simulate() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== Cholesky Decomposition == | |||
This feature performs the [https://en.wikipedia.org/wiki/Cholesky_decomposition Cholesky decomposition] of a positive Hermitian power spectrum matrix and returns the lower triangular matrix (L) of the decomposition. The Cholesky decomposition is a numerical method used to decompose a positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. Specifically, for a matrix | |||
A, the decomposition is given by: | |||
<math display=block>\mathbf{A} = \mathbf{L L}^{*},</math> | |||
<math display=block> L_{j,j} = \sqrt{ A_{j,j} - \sum_{k=1}^{j-1} L_{j,k}^*L_{j,k} }, </math> | |||
<math display=block> L_{i,j} = \frac{1}{L_{j,j}} \left( A_{i,j} - \sum_{k=1}^{j-1} L_{j,k}^* L_{i,k} \right) \quad \text{for } i>j. </math> | |||
where <math>L</math> is a [https://en.wikipedia.org/wiki/Triangular_matrix lower triangular matrix] with real and positive diagonal entries, and <math>L^*</math> denotes the [https://en.wikipedia.org/wiki/Conjugate_transpose conjugate transpose] of <math>L</math>. | |||
The feature is optimized for performance and can handle large matrices efficiently using <math>O(n^3)</math> computational complexity in the worst case. It checks if the input matrix is indeed positive-definite and Hermitian before performing the decomposition and raises an error if the matrix does not meet these conditions. The feature belong to the [[RPS_Feature_Group#PSD_Decomposition_Method|PSD Decomposition Method]] feature group. | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import WindLab | |||
import GeneralToolsGui | |||
import WindLabObjects | |||
from LabRPS import Vector as vec | |||
import LabRPS | |||
import numpy | |||
def compute(): | |||
installResuslt = WindLab.installPlugin("WindLabPlugin") | |||
doc = LabRPS.ActiveDocument | |||
if not doc: | |||
doc = LabRPS.newDocument() | |||
# create WindLab simulation called "Simulation" | |||
sim = WindLabObjects.makeSimulation(doc, "Simulation") | |||
# check if the simulation sucessfully created | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Cholesky Decomposition" | |||
featureGroup = "Spectrum Decomposition Method" | |||
# create the feature | |||
decomposedPSD = WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not decomposedPSD : | |||
LabRPS.Console.PrintError("Error on creating the spectrum decomposition method.\n") | |||
return None | |||
# get the active simulation points feature and compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n") | |||
return None | |||
# use a vector to represent a simulation point based on its coordinates | |||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
v2 = vec(simPoints[1][1], simPoints[1][2], simPoints[1][3]) | |||
v3 = vec(simPoints[2][1], simPoints[2][2], simPoints[2][3]) | |||
# This feature is used to decompose power spectrum matrices which may vary in time. Let's assume that | |||
# the active power spectrun density function in this example is stationary. Meanning it is not varying in time. | |||
#Then, we use time instant of 0 second. | |||
time = 0.0 | |||
# compute the decomposed cross spectrum between points 1 and 3, at time instant of 0 second and for all frequency | |||
# increments. Note that when the following code is run, WindLab will try to identify the active frequency distribution, | |||
# the active power spectrum feature, the active coherence function feature and others. If WindLab fails to find any | |||
# of these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
psd13 = sim.computeDecomposedCrossSpectrumVectorF(v1, v3, time) | |||
# psd13 can be converted to numpy vector and be used for some other purposes. | |||
arr = numpy.asarray(psd13) | |||
compute() | |||
}} | }} | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
Latest revision as of 18:42, 17 January 2025
You can find the source code of this plugin on the following Github repository: Get the code here!. This plugin is one of the official plugins provided by LabRPS. It provides very useful features (tools) for the simulation of random wind velocity. Plugins are very easy to create in LabRPS, therefore, anyone can develop plugin for any random phenomenon in LabRPS. Go to this page to see how to create new plugin for LabRPS. You can get quick assistance from LabRPS community by sending your concern to the community forum.
Horizontal Uniform Distribution
This feature provides an efficient method to distribute random wind simulation points uniformly in space. It allows users to generate a set of points within a 3D spatial domain, ensuring that the points are evenly distributed along a horizontal line that is parallel to one of the coordinate system axis. This uniform distribution is critical in certain simulation methods. For [math]\displaystyle{ n }[/math] simulation points [math]\displaystyle{ (P_1,P_2,P_3,...,P_n) }[/math], the distance [math]\displaystyle{ d_{jk} }[/math] between points [math]\displaystyle{ P_j }[/math] and [math]\displaystyle{ P_k }[/math] must be given by the following formula:
[math]\displaystyle{ d_{jk} = s\times|j-k| }[/math]
where [math]\displaystyle{ s }[/math] is the even space between any two adjacent points.
Properties
- DataFirstPoint: This is a point in 3D space representing the first point the distribution will start from.
- DataSpacing: This is the even space between any two adjacent points in the distribution.
Scripting
import WindLab
import GeneralToolsGui
import WindLabObjects
from LabRPS import Vector as vec
import numpy
import LabRPS
def compute():
installResuslt = WindLab.installPlugin("WindLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create WindLab simulation called "Simulation"
sim = WindLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation sucessfully created
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Horizontal Distribution"
featureGroup = "Location Distribution"
# create the feature
newFeature= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not newFeature:
LabRPS.Console.PrintError("Error on creating the feature.\n")
return None
# let's set the first point of the distribution (x =0, y = 0, z = 80m)
newFeature.FirstPoint = vec(0,0,80000)
# let's set the spacing (s = 10m)
newFeature.Spacing = '10m'
# compute the simulation points coordinates. WindLab will internally use the "newFeature" feature.
simPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(simPoints)
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False)
compute()
Vertical Uniform Distribution
This feature provides an efficient method to distribute random wind simulation points uniformly in space. It allows users to generate a set of points within a 3D spatial domain, ensuring that the points are evenly distributed along a vertical line. This uniform distribution is critical in certain simulation methods. For [math]\displaystyle{ n }[/math] simulation points [math]\displaystyle{ (P_1,P_2,P_3,...,P_n) }[/math], the distance [math]\displaystyle{ d_{jk} }[/math] between points [math]\displaystyle{ P_j }[/math] and [math]\displaystyle{ P_k }[/math] must be given by the following formula:
[math]\displaystyle{ d_{jk} = s\times|j-k| }[/math]
where [math]\displaystyle{ s }[/math] is the even space between any two adjacent points.
Properties
- DataLowestPoint: This is a point in 3D space representing the lowest point the distribution will start from. In many applications, this point should not be lower than 10 meters.
- DataSpacing: This is the even space between any two adjacent points in the distribution.
Scripting
import WindLab
import GeneralToolsGui
import WindLabObjects
from LabRPS import Vector as vec
import numpy
import LabRPS
def compute():
installResuslt = WindLab.installPlugin("WindLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create WindLab simulation called "Simulation"
sim = WindLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation sucessfully created
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Vertical Distribution"
featureGroup = "Location Distribution"
# create the feature
newFeature= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not newFeature:
LabRPS.Console.PrintError("Error on creating the feature.\n")
return None
# let's set the first point of the distribution (x =0, y = 0, z = 30m)
newFeature.LowestPoint = vec(0,0,30000)
# let's set the spacing (s = 10m)
newFeature.Spacing = '10m'
# compute the simulation points coordinates. WindLab will internally use the "newFeature" feature.
simPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(simPoints)
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False)
compute()
Uniform Distribution
This feature may be seen as a general form of the horizontal and the vertical distribution features. It allows users to generate a set of points within a 3D spatial domain, ensuring that the points are evenly distributed along a line parallel to one of the coordinate system axis. For [math]\displaystyle{ n }[/math] simulation points [math]\displaystyle{ (P_1,P_2,P_3,...,P_n) }[/math], the distance [math]\displaystyle{ d_{jk} }[/math] between points [math]\displaystyle{ P_j }[/math] and [math]\displaystyle{ P_k }[/math] must be given by the following formula:
[math]\displaystyle{ d_{jk} = s\times|j-k| }[/math]
where [math]\displaystyle{ s }[/math] is the even space between any two adjacent points.
Properties
- DataFirstPoint: This is a point in 3D space representing the first point the distribution will start from. This should be the lowest point in case the distribution is parallel to the vertical axis and should not be lower than 10 meters in many application.
- DataSpacing: This is the even space between any two adjacent points in the distribution.
- DataDirection: Its value can be X, Y or Z. This is the axis the points distribution is parallel to.
Scripting
This feature can be used to produce vertical distribution as we did before in the Vertical Distribution feature.
import WindLab
import GeneralToolsGui
import WindLabObjects
from LabRPS import Vector as vec
import numpy
import LabRPS
def compute():
installResuslt = WindLab.installPlugin("WindLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create WindLab simulation called "Simulation"
sim = WindLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Uniform Distribution"
featureGroup = "Location Distribution"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
unifSimPoints= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not unifSimPoints:
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n")
# abord the computation
# set the direction of the distribution to be vertical
unifSimPoints.Direction= 'Z'
# let's set the first point of the distribution (x =0, y = 0, z = 30m)
unifSimPoints.FirstPoint = vec(0,0,30000) # This is the lowest point in this case (Direction = 'Z')
# let's set the spacing (s = 10m)
unifSimPoints.Spacing = '10m'
# compute the simulation points coordinates. WindLab will internally use the "unifSimPoints" feature.
simPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(simPoints)
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False)
compute()
Grid Points
This feature allows users to generate a set of grid points within a 3D spatial domain, ensuring that the points are evenly distributed in a plane parallel to one of the coordinate system planes (XY Plane, YZ Plane, XZ Plane).
Properties
- DataSpacing1: This is the points spacing along one of the axis forming the plane.
- DataSpacing2: This is the points spacing along the second axis.
- DataLength1: This is the length within points are distributed along one of the axis forming the plane.
- DataLength2: This is the length within points are distributed along the second axis.
- DataCenterPoint: This is the center of the grid around which the points are generated. It is a 3D point.
- DataNumberOfPoints: This is the resulting total number of points in the grid. This is a read only property for internal use. User cannot change its value directly.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import GeneralToolsGui
import WindLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def compute():
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Grid Points"
featureGroup = "Location Distribution"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
unifSimPoints= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not unifSimPoints:
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n")
# abord the computation
# set the plan the points grid is parallel to
unifSimPoints.LocationPlan= 'YZ Plane'
# let's set the center point of the distribution (x =0, y = 0, z = 0)
unifSimPoints.CenterPoint = vec(0,0,0)
# let's set the spacing1 (s1 = 10m)
unifSimPoints.Spacing1 = '10m'
# let's set the spacing2 (s2 = 10m)
unifSimPoints.Spacing2 = '10m'
# let's set the length1 (l1 = 200m)
unifSimPoints.Length1= '200m'
# let's set the length2 (l2 = 200m)
unifSimPoints.Length2= '200m'
# compute the simulation points coordinates. WindLab will internally use the "unifSimPoints" feature.
simPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(simPoints)
# Example 3D points
x = arr[:,1]
y = arr[:,2]
z = arr[:,3]
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False)
# Create a figure
fig = plt.figure()
# Add 3D axes
ax = fig.add_subplot(111, projection='3d')
# Plot points
ax.scatter(x, y, z, color='blue')
# Hide all axes and labels
ax.set_axis_off()
# Set the title
ax.set_title('3D Plotting of Points')
# Show the plot
plt.show()
compute()
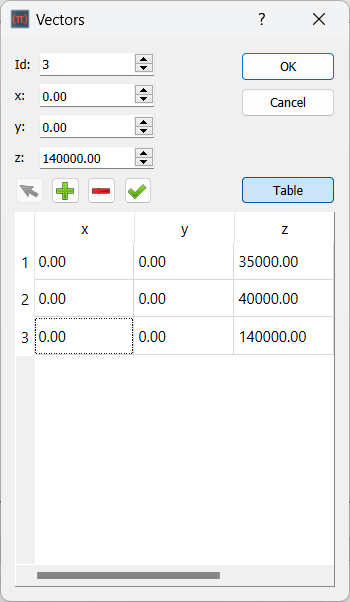
General Distribution
When the simulation points distribution is more general and does not follow any of the previous uniform distribution, this feature can be used. This feature allows users to input simulation points one by one using their coordinates based on the vector dialog shown below:
Properties
- DataLocations: This is a list holding the simulation points
Scripting
The following script shows how this feature can be created and used.
import WindLab
import GeneralToolsGui
import WindLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
def compute():
installResuslt = WindLab.installPlugin("WindLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create WindLab simulation called "Simulation"
sim = WindLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "General Distribution"
featureGroup = "Location Distribution"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
genSimPoints= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not genSimPoints:
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n")
# abord the computation
# create the simulation points by their coordinates
v1 = vec(0, 0, 35000)
v2 = vec(0, 0, 40000)
v3 = vec(0, 0, 140000)
# add the points to the locations
genSimPoints.Locations = [v1, v2, v3]
# compute the simulation points coordinates. WindLab will internally use the "genSimPoints" feature
simPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(simPoints)
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False)
compute()
Import Simulation Points from File
When the simulation points are stored in a file, this feature can be used. The feature allows users to import simulation points coordinates from file. Note that, for now only tab separated text file is supported and the file is expected to have number of rows and number of columns which are number of simulation points and four, respectively.
Properties
- DataFilePath: This is the path to the file.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import GeneralToolsGui
import WindLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
def compute():
installResuslt = WindLab.installPlugin("WindLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create WindLab simulation called "Simulation"
sim = WindLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Import Simulation Points from File"
featureGroup = "Location Distribution"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
simPoints= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not simPoints:
LabRPS.Console.PrintError("Error on creating the simulation points feature.\n")
# abord the computation
# set the direction of the distribution to be vertical
simPoints.FilePath = "D:/Points.txt"
# compute the simulation points coordinates. WindLab will internally use the "simPoints" feature.
importedSimPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(importedSimPoints )
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, importedSimPoints, False)
compute()
Power Law Profile
This feature is designed to compute the wind speed at a given height based on the power law mean wind profile, which is commonly used to model the variation of wind speed with height in the atmospheric boundary layer. This model is essential in fields such as wind energy, structural engineering, and environmental science. The power law formula that governs the relationship between wind speed and height is expressed as:
[math]\displaystyle{ U(z) = U(z_0)\times\left( \frac{{z-\phi}}{z_0} \right)^\alpha }[/math]
where:
- [math]\displaystyle{ U(z) }[/math] is the wind speed at height [math]\displaystyle{ z }[/math],
- [math]\displaystyle{ U(z_0) }[/math] is the reference wind speed at a known reference height [math]\displaystyle{ z_0 }[/math],
- [math]\displaystyle{ \alpha }[/math] is the power law exponent, a dimensionless constant that varies depending on terrain and atmospheric conditions,
- [math]\displaystyle{ \phi }[/math] is the zero plan displacement,
- [math]\displaystyle{ z }[/math] is the height at which the wind speed is to be calculated.
Properties
- DataReferenceHeight: This is a reference height.
- DataReferenceSpeed: This is the reference wind speed at the reference height.
- DataDimensionlessPower: This is the power law exponent.
- DataZeroPlanDisplacement: This is the zero plan displacement.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import GeneralToolsGui
import WindLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
def compute():
installResuslt = WindLab.installPlugin("WindLabPlugin")
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Power Law Profile"
featureGroup = "Mean Wind Profile"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
meanSpeed= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not meanSpeed:
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n")
# abord the computation
meanSpeed.ReferenceHeight = '10.00 m'
meanSpeed.ReferenceSpeed = '30.00 m/s'
meanSpeed.DimensionlessPower = 0.12
meanSpeed.ZeroPlanDisplacement = '0.0 m'
# In WindLab, mean wind velocity can vary with time. In case the user desires a time dependent mean wind speed,
# a modulation function can be used for this purpose. The feature account for this. When the Stationarity property of the parent
# simulation of this feature is false, the feature identify the active modulation function and use it to produce non-stationary
# mean wind speed. But for this example we shall use time instant of 0 second.
time = 0.0
# compute the mean wind speeds at time instant of 0 second and for all simulation points
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
meanValues = sim.computeMeanWindSpeedVectorP(time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(meanValues )
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 2, meanValues, False)
compute()
Logarithmic Law Profile
This feature is designed to compute the wind speed at a given height based on the logarithmic law mean wind profile. The logarithmic law is commonly used to model the variation of wind speed with height in the atmospheric boundary layer, especially in cases where the wind profile is influenced by surface roughness, such as over flat terrain, forests, or urban environments. The logarithmic law for wind speed variation is given by the following equation:
[math]\displaystyle{ U(z) =\left( \frac{u_*}{k} \right)\times\ln{\left( \frac{{z-\phi}}{z_0} \right)} }[/math]
where:
- [math]\displaystyle{ U(z) }[/math] is the wind speed at height [math]\displaystyle{ z }[/math],
- [math]\displaystyle{ u_* }[/math] is the friction velocity, which is a measure of the turbulence intensity,
- [math]\displaystyle{ k }[/math] is the von Kármán constant (approximately 0.4),
- [math]\displaystyle{ \phi }[/math] is the zero plan displacement,
- [math]\displaystyle{ z_0 }[/math] is the roughness length, which characterizes the roughness of the surface,
- [math]\displaystyle{ z }[/math] is the height at which the wind speed is to be calculated.
Properties
- DataTerrainRoughness: This is the terrain roughness value.
- DataShearVelocity: This is the shear velocity of the flow.
- DatavonKarmanConstant: This is the von karman constant.
- DataZeroPlanDisplacement: This is the zero plan displacement value.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Logarithmic Law Profile"
featureGroup = "Mean Wind Profile"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
meanSpeed= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not meanSpeed:
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n")
# abord the computation
meanSpeed.TerrainRoughness = '0.001266 m'
meanSpeed.ShearVelocity = '1.76 m/s'
# In WindLab, mean wind velocity can vary with time. In case the user desires a time dependent mean wind speed,
# a modulation function can be used for this purpose. The feature account for this. When the Stationarity property of the parent
# simulation of this feature is false, the feature identify the active modulation function and use it to produce non-stationary
# mean wind speed. But for this example we shall use time instant of 0 second.
time = 0.0
# compute the mean wind speeds at time instant of 0 second and for all simulation points
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
meanValues = sim.computeMeanWindSpeedVectorP(time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(meanValues )
Deaves and Harris Profile
This feature is designed to compute the wind speed at a given height based on the logarithmic law mean wind profile. The logarithmic law is commonly used to model the variation of wind speed with height in the atmospheric boundary layer, especially in cases where the wind profile is influenced by surface roughness, such as over flat terrain, forests, or urban environments. The logarithmic law for wind speed variation is given by the following equation:
[math]\displaystyle{ U(z) =\left( \frac{u_*}{k} \right)\times\left [\ln{\left( \frac{{z-z_d}}{z_0} \right)} + 5.75\left( \frac{{z-z_d}}{h} \right) - 1.88\left( \frac{{z-z_d}}{h} \right)^2 - 1.33\left( \frac{{z-z_d}}{h} \right)^3 + 0.25\left( \frac{{z-z_d}}{h} \right)^4\right ] }[/math]
where:
- [math]\displaystyle{ U(z) }[/math] is the wind speed at height [math]\displaystyle{ z }[/math],
- [math]\displaystyle{ u_* }[/math] is the friction velocity, which is a measure of the turbulence intensity,
- [math]\displaystyle{ k }[/math] is the von Kármán constant (approximately 0.4),
- [math]\displaystyle{ z_d }[/math] is the zero plan displacement,
- [math]\displaystyle{ z_0 }[/math] is the roughness length, which characterizes the roughness of the surface,
- [math]\displaystyle{ h }[/math] is the gradient height, defined as the height where atmospheric flow is free from surface stresses and becomes geostrophic,
- [math]\displaystyle{ z }[/math] is the height at which the wind speed is to be calculated.
Properties
- DataTerrainRoughness: The terrain roughness length.
- DataShearVelocity: The shear velocity of the flow.
- DataZeroPlanDisplacement: The zero plan displacement.
- DataLatitude: The latitude.
- DataEarthAngularVelocity: The earth angular velocity.
- DataBetta: The coefficient beta.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Deaves and Harris Profile"
featureGroup = "Mean Wind Profile"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
meanSpeed= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not meanSpeed:
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n")
# abord the computation
meanSpeed.TerrainRoughness = '0.001266 m'
meanSpeed.ShearVelocity = '1.76 m/s'
# In WindLab, mean wind velocity can vary with time. In case the user desires a time dependent mean wind speed,
# a modulation function can be used for this purpose. The feature account for this. When the Stationarity property of the parent
# simulation of this feature is false, the feature identify the active modulation function and use it to produce non-stationary
# mean wind speed. But for this example we shall use time instant of 0 second.
time = 0.0
# compute the mean wind speeds at time instant of 0 second and for all simulation points
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
meanValues = sim.computeMeanWindSpeedVectorP(time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(meanValues )
Sine Modulation Function
This feature represents a uniform modulation function used to achieve stationarity in the simulation of random wind velocity. Uniformity here means the modulation function is not function of frequency. It is modeled as a sine wave, described by the following equation:
[math]\displaystyle{ A(t) = sin\left( \frac{\pi\times t}{T} \right) }[/math]
where:
- [math]\displaystyle{ A(t) }[/math] is the modulation function value at time [math]\displaystyle{ t }[/math],
- [math]\displaystyle{ T }[/math] is the pulse duration,
- [math]\displaystyle{ t }[/math] is the time at which the modulation function is computed.
Properties
- DataPulseDuration: The pusle duration.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Sine Wave Modulation Function"
featureGroup = "Uniform Modulation Function"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
modulation= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not modulation:
LabRPS.Console.PrintError("Error on creating the modulation function feature.\n")
# abord the computation
modulation.PulseDuration= '150 m/s'
# set a time instant of 2 seconds
time = 2
# compute the modulation value at time instant of 2 second and for all simulation points
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# If WindLab fails to find this dependency feature, the computation will fails and specific error messages will be sent to the report view.
modulations= sim.computeModulationVectorP(time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(modulations)
Three Parameter Modulation Function
This feature represents a uniform modulation function used to achieve stationarity in the simulation of random wind velocity. Uniformity here means the modulation function is not function of frequency. It is modeled as an exponential function, described by the following equation:
[math]\displaystyle{ A(t) = \alpha t^\beta e^{-\lambda t} }[/math]
where:
- [math]\displaystyle{ A(t) }[/math] is the modulation function value at time [math]\displaystyle{ t }[/math],
- [math]\displaystyle{ \alpha }[/math] is the alpha coefficient,
- [math]\displaystyle{ \beta }[/math] is the beta coefficient,
- [math]\displaystyle{ \lambda }[/math] is the lambda coefficient,
- [math]\displaystyle{ t }[/math] is the time at which the modulation function is computed.
Properties
- DataAlpha: The alpha coefficient.
- DataBetta: The beta coefficient.
- DataLambda: The lambda coefficient.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Three Parameter Modulation Function"
featureGroup = "Uniform Modulation Function"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
modulation= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not modulation:
LabRPS.Console.PrintError("Error on creating the modulation function feature.\n")
# abord the computation
modulation.Alpha = 4.98
modulation.Betta = 3.00
modulation.Lambda = 0.003
# set a time instant of 2 seconds
time = 2
# compute the modulation value at time instant of 2 second and for all simulation points
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# If WindLab fails to find this dependency feature, the computation will fails and specific error messages will be sent to the report view.
modulations= sim.computeModulationVectorP(time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(modulations)
Exponential Modulation Function
This feature represents a uniform modulation function used to achieve stationarity in the simulation of random wind velocity. Uniformity here means the modulation function is not function of frequency. It is modeled as an exponential function, described by the following equation:
[math]\displaystyle{ A(t) = exp\left[-\frac{1}{2}\left( \frac{t-t_{m} }{t_{l}} \right)^2\right] }[/math]
where:
- [math]\displaystyle{ A(t) }[/math] is the modulation function value at time [math]\displaystyle{ t }[/math],
- [math]\displaystyle{ t_{m} }[/math] is the time when the modulation function reaches its maximum,
- [math]\displaystyle{ t_{l} }[/math] is the storm length,
- [math]\displaystyle{ t }[/math] is the time at which the modulation function is computed.
Properties
- DataTimeOfMax: The time when the modulation function reaches its maximum.
- DataStormLength: The storm length.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Exponential Modulation Function"
featureGroup = "Uniform Modulation Function"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
modulation= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not modulation:
LabRPS.Console.PrintError("Error on creating the modulation function feature.\n")
# abord the computation
modulation.TimeOfMax = '300 s'
modulation.StormLength = '60 s'
# set a time instant of 2 seconds
time = 2
# compute the modulation value at time instant of 2 second and for all simulation points
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# If WindLab fails to find this dependency feature, the computation will fails and specific error messages will be sent to the report view.
modulations= sim.computeModulationVectorP(time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(modulations)
Davenport Coherence Function
The purpose of this feature is to model the spatial correlation of wind velocities, which is crucial in many engineering applications, especially in the context of wind turbine design, structural analysis, and environmental studies. The Davenport Coherence Function quantifies the correlation between the wind velocity at two points, in space (at different locations). It is derived from the theory of wind turbulence and helps in simulating the correlated behavior of wind speeds over a geographical area. The mathematical form of the Davenport Coherence Function, for two points [math]\displaystyle{ P_{j}\left( x_{j},y_{j},z_{j} \right) }[/math] and [math]\displaystyle{ P_{k}\left( x_{k},y_{k},z_{k} \right) }[/math] is expressed as:
[math]\displaystyle{ \gamma(\omega) = exp\left[-\frac{\omega}{2 \pi}\left( \frac{\sqrt{C_{x}^2 \left( x_{j}-x_{k} \right)^2 + C_{y}^2 \left( y_{j}-y_{k} \right)^2 + C_{z}^2 \left( z_{j}-z_{k} \right)^2}}{\frac{U_{j}\left( z_{j} \right)+U_{k}\left( z_{k} \right)}{2}} \right)\right] }[/math]
where:
- [math]\displaystyle{ \gamma(\omega) }[/math] is the coherence function for two points [math]\displaystyle{ P_{j}\left( x_{j},y_{j},z_{j} \right) }[/math] and [math]\displaystyle{ P_{k}\left( x_{k},y_{k},z_{k} \right) }[/math] value for frequency [math]\displaystyle{ \omega }[/math],
- [math]\displaystyle{ C_{x} }[/math] is the decay coefficient along x,
- [math]\displaystyle{ C_{y} }[/math] is the decay coefficient along y,
- [math]\displaystyle{ C_{z} }[/math] is the decay coefficient along z,
- [math]\displaystyle{ U_{j}\left( z_{j} \right) }[/math] is the mean wind speed at altitude [math]\displaystyle{ z_{j} }[/math],
- [math]\displaystyle{ U_{k}\left( z_{k} \right) }[/math] is the mean wind speed at altitude [math]\displaystyle{ z_{k} }[/math],
- [math]\displaystyle{ \omega }[/math] is the frequency for which the coherence function is computed.
Properties
- DataExponentialDecayCx: The decay coefficient along x.
- DataExponentialDecayCy: The decay coefficient along y
- DataExponentialDecayCz: The decay coefficient along z
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Davenport Coherence Function"
featureGroup = "Coherence Function"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
coherence = WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not coherence:
LabRPS.Console.PrintError("Error on creating the coherence function feature.\n")
# abord the computation
coherence.ExponentialDecayCx = 10.0
coherence.ExponentialDecayCy = 7.0
coherence.ExponentialDecayCz = 6.0
# In WindLab, coherence function can vary with time. In case the user desires a time dependent coherence function,
# a modulation function can be used for this purpose. The feature account for this. When the Stationarity property of the parent
# simulation of this feature is false, the feature identify the active modulation function and use it to produce non-stationary
# coherence function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
coherences = sim.computeCrossCoherenceMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(coherences)
Krenk Coherence Function
Documentation coming soon.
Davenport Along Wind Spectrum
The Davenport spectrum is widely used in wind engineering to model the power spectral density (PSD) of wind velocity in its main direction. The Davenport Power Spectrum or Davenport Wind Spectrum, can be mathematically expressed as:
[math]\displaystyle{ \frac{nS(n)}{u_{*}^2} = k\frac{x^2}{\left(1 + x^2 \right)^{4/3}} }[/math]
where:
- [math]\displaystyle{ x = \frac{1200n}{U_{10}} }[/math],
- [math]\displaystyle{ S(n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ u_{*} }[/math] is the shear velocity of the flow,
- [math]\displaystyle{ k }[/math] is the von Karman constant which is equal to 4.0,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U_{10} }[/math] is the mean wind speed at height of 10 meters.
Properties
- DataMeanWindSpeed10: The mean wind speed at height of 10 meters
- DatashearVelocity: The shear velocity of the flow
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Davenport Along Wind Spectrum"
featureGroup = "Along Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.MeanWindSpeed10= '30.0 m/s'
spectrum.shearVelocity= '1.76 m/s'
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeXCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
Harris Along Wind Spectrum
The Harris spectrum is widely used in wind engineering to model the power spectral density (PSD) of wind velocity in its main direction. The Harris Power Spectrum or Harris Wind Spectrum, can be mathematically expressed as:
[math]\displaystyle{ \frac{nS(n)}{u_{*}^2} = k\frac{x^2}{\left(2 + x^2 \right)^{5/6}} }[/math]
where:
- [math]\displaystyle{ x = \frac{1800n}{U_{10}} }[/math],
- [math]\displaystyle{ S(n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ u_{*} }[/math] is the shear velocity of the flow,
- [math]\displaystyle{ k }[/math] is the von Karman constant which is equal to 4.0,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U_{10} }[/math] is the mean wind speed at height of 10 meters.
Properties
- DataMeanWindSpeed10: The mean wind speed at height of 10 meters
- DatashearVelocity: The shear velocity of the flow
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Harris Along Wind Spectrum"
featureGroup = "Along Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.MeanWindSpeed10= '30.0 m/s'
spectrum.shearVelocity= '1.76 m/s'
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeXCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
Kaimal Along Wind Spectrum
The Kaimal Spectrum is a frequency-domain model that describes the distribution of energy in turbulent wind velocity across different frequencies. It is specifically designed for modeling atmospheric turbulence. The Kaimal model provides a power spectral density (PSD) function that approximates the energy contained in the wind velocity as a function of frequency. Mathematically, the Kaimal along wind spectrum is given by:
[math]\displaystyle{ \frac{nS(z,n)}{u_{*}^2} = \frac{200f}{\left(1 + 50f \right)^{5/3}} }[/math]
where:
- [math]\displaystyle{ f = \frac{nz}{U(z)} }[/math],
- [math]\displaystyle{ S(z,n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ u_{*} }[/math] is the shear velocity of the flow,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U(z) }[/math] is the mean wind speed at height [math]\displaystyle{ z }[/math].
Properties
- DatashearVelocity: The shear velocity of the flow
- DataConstant1: A constant equal to 200.0 by default
- DataConstant2: A constant equal to 50.0 by default
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Kaimal Along Wind Spectrum"
featureGroup = "Along Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.shearVelocity= '1.76 m/s'
spectrum.Constant1 = 200.0
spectrum.Constant2 = 50.0
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeXCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
Kaimal Across Wind Spectrum
The Kaimal Spectrum is a frequency-domain model that describes the distribution of energy in turbulent wind velocity across different frequencies. It is specifically designed for modeling atmospheric turbulence. The Kaimal model provides a power spectral density (PSD) function that approximates the energy contained in the wind velocity as a function of frequency. Mathematically, the Kaimal across wind spectrum is given by:
[math]\displaystyle{ \frac{nS(z,n)}{u_{*}^2} = \frac{15f}{\left(1 + 9.5f \right)^{5/3}} }[/math]
where:
- [math]\displaystyle{ f = \frac{nz}{U(z)} }[/math],
- [math]\displaystyle{ S(z,n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ u_{*} }[/math] is the shear velocity of the flow,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U(z) }[/math] is the mean wind speed at height [math]\displaystyle{ z }[/math].
Properties
- DatashearVelocity: The shear velocity of the flow
- DataConstant1: A constant equal to 15.0 by default
- DataConstant2: A constant equal to 9.5 by default
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Kaimal Across Wind Spectrum"
featureGroup = "Across Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.shearVelocity= '1.76 m/s'
spectrum.Constant1 = 15.0
spectrum.Constant2 = 9.5
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeYCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
Kaimal Vertical Wind Spectrum
The Kaimal Spectrum is a frequency-domain model that describes the distribution of energy in turbulent wind velocity across different frequencies. It is specifically designed for modeling atmospheric turbulence. The Kaimal model provides a power spectral density (PSD) function that approximates the energy contained in the wind velocity as a function of frequency. Mathematically, the Kaimal vertical spectrum is given by:
[math]\displaystyle{ \frac{nS(z,n)}{u_{*}^2} = \frac{3.36f}{1 + 10f^{5/3}} }[/math]
where:
- [math]\displaystyle{ f = \frac{nz}{U(z)} }[/math],
- [math]\displaystyle{ S(z,n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ u_{*} }[/math] is the shear velocity of the flow,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U(z) }[/math] is the mean wind speed at height [math]\displaystyle{ z }[/math].
Properties
- DatashearVelocity: The shear velocity of the flow
- DataConstant1: A constant equal to 3.36 by default
- DataConstant2: A constant equal to 10.0 by default
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Kaimal Vertical Wind Spectrum"
featureGroup = "Vertical Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.shearVelocity= '1.76 m/s'
spectrum.Constant1 = 3.36
spectrum.Constant2 = 10.0
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeZCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
Simiu Along Wind Spectrum
The Simiu Spectrum is a frequency-domain model that describes the distribution of energy in turbulent wind velocity across different frequencies. It is specifically designed for modeling atmospheric turbulence. The Simiu model provides a power spectral density (PSD) function that approximates the energy contained in the wind velocity as a function of frequency. Mathematically, the Simiu along wind spectrum is given by:
[math]\displaystyle{ \frac{nS(z,n)}{u_{*}^2} = \frac{105f}{\left(1 + 33f \right)^{5/3}} }[/math]
where:
- [math]\displaystyle{ f = \frac{nz}{U(z)} }[/math],
- [math]\displaystyle{ S(z,n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ u_{*} }[/math] is the shear velocity of the flow,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U(z) }[/math] is the mean wind speed at height [math]\displaystyle{ z }[/math].
Properties
- DatashearVelocity: The shear velocity of the flow
- DataConstant1: A constant equal to 105.0 by default
- DataConstant2: A constant equal to 33.0 by default
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Simiu Along Wind Spectrum"
featureGroup = "Along Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.shearVelocity= '1.76 m/s'
spectrum.Constant1 = 105.0
spectrum.Constant2 = 33.0
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeXCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
Simiu Across Wind Spectrum
The Simiu Spectrum is a frequency-domain model that describes the distribution of energy in turbulent wind velocity across different frequencies. It is specifically designed for modeling atmospheric turbulence. The Simiu model provides a power spectral density (PSD) function that approximates the energy contained in the wind velocity as a function of frequency. Mathematically, the Simiu across wind spectrum is given by:
[math]\displaystyle{ \frac{nS(z,n)}{u_{*}^2} = \frac{17f}{\left(1 + 9.5f \right)^{5/3}} }[/math]
where:
- [math]\displaystyle{ f = \frac{nz}{U(z)} }[/math],
- [math]\displaystyle{ S(z,n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ u_{*} }[/math] is the shear velocity of the flow,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U(z) }[/math] is the mean wind speed at height [math]\displaystyle{ z }[/math].
Properties
- DatashearVelocity: The shear velocity of the flow
- DataConstant1: A constant equal to 17.0 by default
- DataConstant2: A constant equal to 9.5 by default
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Simiu Across Wind Spectrum"
featureGroup = "Across Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.shearVelocity= '1.76 m/s'
spectrum.Constant1 = 17.0
spectrum.Constant2 = 9.5
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeYCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
Simiu Vertical Wind Spectrum
The Simiu Spectrum is a frequency-domain model that describes the distribution of energy in turbulent wind velocity across different frequencies. It is specifically designed for modeling atmospheric turbulence. The Simiu model provides a power spectral density (PSD) function that approximates the energy contained in the wind velocity as a function of frequency. Mathematically, the Simiu vertical spectrum is given by:
[math]\displaystyle{ \frac{nS(z,n)}{u_{*}^2} = \frac{2f}{1 + 5.3f^{5/3}} }[/math]
where:
- [math]\displaystyle{ f = \frac{nz}{U(z)} }[/math],
- [math]\displaystyle{ S(z,n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ u_{*} }[/math] is the shear velocity of the flow,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U(z) }[/math] is the mean wind speed at height [math]\displaystyle{ z }[/math].
Properties
- DatashearVelocity: The shear velocity of the flow
- DataConstant1: A constant equal to 2 by default
- DataConstant2: A constant equal to 5.3 by default
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Simiu Vertical Wind Spectrum"
featureGroup = "Vertical Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.shearVelocity= '1.76 m/s'
spectrum.Constant1 = 2
spectrum.Constant2 = 5.3
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeZCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
von Karman Along Wind Spectrum
The von Karman Spectrum is a frequency-domain model that describes the distribution of energy in turbulent wind velocity across different frequencies. It is specifically designed for modeling atmospheric turbulence. The von Karman model provides a power spectral density (PSD) function that approximates the energy contained in the wind velocity as a function of frequency. Mathematically, the von Karman along wind spectrum is given by:
[math]\displaystyle{ \frac{nS(z,n)}{\sigma_{u}^2} = \frac{4f}{\left(1 + 70.8f^2 \right)^{5/6}} }[/math]
where:
- [math]\displaystyle{ f = \frac{nL_u}{U(z)} }[/math],
- [math]\displaystyle{ S(z,n) }[/math] is the power spectral density value for frequency value [math]\displaystyle{ n }[/math],
- [math]\displaystyle{ \sigma_{u} }[/math] is the standard deviation,
- [math]\displaystyle{ n }[/math] is the frequency for which the power spectral density is computed.
- [math]\displaystyle{ U(z) }[/math] is the mean wind speed at height [math]\displaystyle{ z }[/math].
Properties
- DataStandardDeviation: The standard deviation
- DataIntegralLengthScale: The integral length scale
- DataConstant1: A constant equal to 4.0 by default
- DataConstant2: A constant equal to 70.8.0 by default
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "von Karman Along Wind Spectrum"
featureGroup = "Along Wind Spectrum"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
spectrum= WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum feature.\n")
# abord the computation
spectrum.StandardDeviation = '1 m/s'
spectrum.IntegralLengthScale = '80 m'
spectrum.Constant1 = 4.0
spectrum.Constant2 = 70.8.0
# In WindLab, power spectral density function can vary with time. In case the user desires a time dependent spectrum function,
# a modulation function can be used for this purpose if the feature is stationary and allows uniform modulation.
# The feature account for this. When the Stationarity property of the parent simulation of this feature is false,
# the feature identify the active modulation function and use it to produce non-stationary
# spectrum function by transforming the the mean wind speeds into time dependent mean wind speeds. But for this example we shall use time instant of 0 second.
time = 0.0
frequency = 0.25
# compute the coherence matrix at time instant of 0 second and frequency of 0.24 rad/s
# Note that when the following code is run, WindLab will try to identify the active locations distribution,
# it will also try to identity the active modulation function in case the parent simulation is non-stationary.
# If WindLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrumMatrix = sim.computeXCrossSpectrumMatrixPP(frequency, time)
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(spectrumMatrix)
Uniform Random Phases
In the simulation of random wind velocity, one common technique is to represent the wind velocity as a sum of multiple sinusoidal components in the frequency domain. Each of these components is associated with a random phase, which determines the position of the sine wave relative to time. By assigning uniform random phases to each frequency component, the resulting time series will have random characteristics, while still adhering to the desired spectral properties, such as a specific power spectral density (PSD) or turbulence spectrum. The feature generate [math]\displaystyle{ n }[/math] sequences [math]\displaystyle{ (\phi_{1l}, \phi_{2l}, \phi_{3l},..., \phi_{nl}; l = 1, 2, 3, ..., N) }[/math] of independent random phase angles uniformly distributed over the interval [math]\displaystyle{ [0, 2\pi] }[/math] by default.
Properties
- DataMinimumValue: The minimum value that can be generated
- DataMaximumValue: The maximum value that can be generated
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Uniform Random Phases"
featureGroup = "Randomness Provider"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
randomness = WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not randomness:
LabRPS.Console.PrintError("Error on creating the randomness feature.\n")
# abord the computation
randomness.MinimumValue = 0
randomness.MaximumValue = 6.28
# generate random phase angle
randomnessMatrix = sim.generateRandomMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(randomnessMatrix)
Uniform Random Phases Import
When the simulation numbers are stored in a file, this feature can be used. The feature allows users to import random numbers from file. Note that, for now only tab separated text file is supported and the file is expected to have number of rows and number of columns which are number of frequency increments and number of simulation points, respectively.
Properties
- DataFilePath: This is the path to the file.
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Uniform Random Phases Import"
featureGroup = "Randomness Provider"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
randomness = WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not randomness:
LabRPS.Console.PrintError("Error on creating the randomness feature.\n")
# abord the computation
randomness.FilePath = "myfolderpath/myfile.txt"
# generate random phase angle
randomnessMatrix = sim.generateRandomMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(randomnessMatrix)
Single Index Frequency Discretization
This feature allows to discretize continuous frequency according to the following formula:
[math]\displaystyle{ \omega_{l} = l\Delta\omega; \quad l = 1, 2, 3, ..., N }[/math].
where:
- [math]\displaystyle{ \Delta\omega }[/math] is the frequency increment,
- [math]\displaystyle{ N }[/math] is the number of frequency increments,
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Single Index Frequency Discretization"
featureGroup = "Frequency Distribution"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
frequency = WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not frequency:
LabRPS.Console.PrintError("Error on creating the frequency feature.\n")
# abord the computation
# compute the freqency distribution
frequencyMatrix = sim.computeFrequenciesMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(frequencyMatrix)
Double Index Frequency Discretization
This feature allows to discretize continuous frequency according to the following formula:
[math]\displaystyle{ \omega_{ml} = (l-1)\Delta\omega + \frac{m}{n}\Delta\omega; \quad m = 1, 2, 3, ..., n; \quad l = 1, 2, 3, ..., N }[/math].
where:
- [math]\displaystyle{ \Delta\omega }[/math] is the frequency increment,
- [math]\displaystyle{ n }[/math] is the number of simulation points,
- [math]\displaystyle{ N }[/math] is the number of frequency increments,
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Double Index Frequency Discretization"
featureGroup = "Frequency Distribution"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
frequency = WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not frequency:
LabRPS.Console.PrintError("Error on creating the frequency feature.\n")
# abord the computation
# compute the freqency distribution
frequencyMatrix = sim.computeFrequenciesMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(frequencyMatrix)
Zerva Frequency Discretization
This feature allow to discretize continuous frequency according to the following formula:
[math]\displaystyle{ \omega_{l} = (1+\frac{l}{2})\Delta\omega;\quad l = 1, 2, 3, ..., N }[/math],
where:
- [math]\displaystyle{ \Delta\omega }[/math] is the frequency increment,
- [math]\displaystyle{ N }[/math] is the number of frequency increments,
Scripting
The following script shows how this feature can be created and used.
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing WindLab simulation called "Simulation"
sim = WindLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Zerva Frequency Discretization"
featureGroup = "Frequency Distribution"
# create the feature and add it to the existing simulation (you may refer to the WindLab Workbench page in
# case you don't understand the next line)
frequency = WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not frequency:
LabRPS.Console.PrintError("Error on creating the frequency feature.\n")
# abord the computation
# compute the freqency distribution
frequencyMatrix = sim.computeFrequenciesMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(frequencyMatrix)
George Deodatis Simulation Method 1996
The paper "Simulation of Ergodic Multivariate Stochastic Processes" by G. Deodatis (1996) presents a method for simulating multivariate stochastic processes, particularly focusing on ergodic processes. The goal of the paper is to provide an efficient method to simulate multivariate stochastic processes that are ergodic. Ergodic processes are those where time averages of the process can be taken as realizations of the ensemble averages. The method is applicable to a wide range of stochastic processes, particularly those in engineering and environmental sciences (e.g., wind, seismic activity, or oceanography). According to the method, the stochastic process [math]\displaystyle{ f_{j}(t) (j = 1, 2, 3, ..., n) }[/math] can be simulated by the following series as:
[math]\displaystyle{ f_{j}(t) = 2\sum_{m=1}^{n}\sum_{l=1}^{N}|H_{jm}(\omega_{ml})|\sqrt{\Delta\omega}\cos\left[\omega_{ml}t+\theta_{jm}(\omega_{ml})+\Phi_{ml}\right];\quad j = 1, 2, 3, ..., n;\quad l = 1, 2, 3, ..., N }[/math]
where:
- [math]\displaystyle{ S(\omega) = H(\omega)H^{T*}(\omega) }[/math],
- [math]\displaystyle{ \theta_{jm}(\omega_{ml}) = tan^{-1}\left(\frac{Im[H_{jm}(\omega_{ml})]}{Re[H_{jm}(\omega_{ml})]}\right) }[/math],
- [math]\displaystyle{ f_{j}(t) }[/math] is the wind velocity at time instant [math]\displaystyle{ t }[/math] and location [math]\displaystyle{ j }[/math],
- [math]\displaystyle{ \Delta\omega }[/math] is the frequency increment,
- [math]\displaystyle{ N }[/math] is the number of frequency increments,
- [math]\displaystyle{ \Phi_{ml} }[/math] are [math]\displaystyle{ n }[/math] sequences of independent random phase angles distributed uniformly over the interval [math]\displaystyle{ \left [ 0,2\pi \right ] }[/math].
Refer to the paper for more details. Not that, in LabRPS this feature depends on some other features such as location distribution, mean wind profile, power spectral density, coherence function among others. These dependent features must me be created first. You can run the feature any time and follow the error messages to identify the missing feature that you need to create. You can also refer to the script below to identify all required features. In case you want to obtain the results as presented in the paper, you need to used all the parameters as presented in the paper.
Scripting
The following script shows how this feature can be created and used.
import LabRPS
import WindLab
import WindLabObjects
from LabRPS import Vector as vec
import time
def simulate():
# Plugin
installResuslt = WindLab.installPlugin("WindLabPlugin")
if not installResuslt:
LabRPS.Console.PrintError("The installation the WindLabPlugin has failed.\n")
return None
# Document
doc = LabRPS.newDocument()
# Simulation
sim = WindLabObjects.makeSimulation(doc, "Simulation")
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
# set simulation parameters
sim.NumberOfFrequency = 2048
sim.MaxFrequency = "0.64 Hz" # 4 rad/s;
sim.FrequencyIncrement = "0.00031 Hz" # 0.00195 rad/s;
sim.TimeIncrement = "0.785 s"
sim.NumberOfTimeIncrements = 9651
# Simulation points
loc = WindLabObjects.makeFeature("SimulationPoints", "Simulation", "General Distribution", "Location Distribution")
if not loc:
LabRPS.Console.PrintError("Error on creating the location distribution.\n")
return None
v1 = vec(0, 0, 35)
v2 = vec(0, 0, 40)
v3 = vec(0, 0, 140)
loc.Locations = [v1, v2, v3]
# Mean wind Profile
mean = WindLabObjects.makeFeature("MeanSpeed", "Simulation", "Logarithmic Law Profile", "Mean Wind Profile")
if not mean:
LabRPS.Console.PrintError("The creation of the mean wind profile was not successuful.\n")
return None
mean.TerrainRoughness = '0.001266 m'
mean.ShearVelocity = '1.76 m/s'
# Frequencies
frequency = WindLabObjects.makeFeature("Frequencies", "Simulation", "Double Index Frequency Discretization", "Frequency Distribution")
if not frequency:
LabRPS.Console.PrintError("Error on creating the frequency distribution.\n")
return None
# Spectrum
spectrum = WindLabObjects.makeFeature("Spectrum", "Simulation", "Kaimal Along Wind Spectrum", "Along Wind Spectrum")
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum model.\n")
return None
# Coherence
coherence = WindLabObjects.makeFeature("CoherenceFunction", "Simulation", "Davenport Coherence Function", "Coherence Function")
if not coherence:
LabRPS.Console.PrintError("The creation of the coherence was not successuful.\n")
return None
coherence.ExponentialDecayCz = 10
# Spectrum decomposition
spectrumD = WindLabObjects.makeFeature("SpectrumDecomposition", "Simulation", "Cholesky Decomposition", "Spectrum Decomposition Method")
if not spectrumD:
LabRPS.Console.PrintError("Error on creating the spectrum decomposition method.\n")
return None
# Random phase
randomness = WindLabObjects.makeFeature("RandomPhases", "Simulation", "Uniform Random Phases", "Randomness Provider")
if not randomness:
LabRPS.Console.PrintError("The creation of the randomness provider was not successuful.\n")
return None
# Simulation method
simMethod = WindLabObjects.makeFeature("SimulationMethod", "Simulation", "Deodatis 1996", "Simulation Method")
if not simMethod:
LabRPS.Console.PrintError("Error on creating the simulation method.\n")
return None
# Run simulation and output the first(0) sample
# store starting time
begin = time.time()
velocities = sim.simulate(0)
# store end time
end = time.time()
LabRPS.Console.PrintMessage(f"Total runtime of the simulaltion is {end - begin} seconds\n")
if LabRPS.GuiUp:
import WindLabGui
import GeneralToolsGui
WindLabGui.setActiveSimulation(sim)
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfTimeIncrements, sim.getSimulationData().numberOfSpatialPosition + 1, velocities, True)
simulate()
Cholesky Decomposition
This feature performs the Cholesky decomposition of a positive Hermitian power spectrum matrix and returns the lower triangular matrix (L) of the decomposition. The Cholesky decomposition is a numerical method used to decompose a positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. Specifically, for a matrix A, the decomposition is given by:
[math]\displaystyle{ \mathbf{A} = \mathbf{L L}^{*}, }[/math]
[math]\displaystyle{ L_{j,j} = \sqrt{ A_{j,j} - \sum_{k=1}^{j-1} L_{j,k}^*L_{j,k} }, }[/math]
[math]\displaystyle{ L_{i,j} = \frac{1}{L_{j,j}} \left( A_{i,j} - \sum_{k=1}^{j-1} L_{j,k}^* L_{i,k} \right) \quad \text{for } i\gt j. }[/math]
where [math]\displaystyle{ L }[/math] is a lower triangular matrix with real and positive diagonal entries, and [math]\displaystyle{ L^* }[/math] denotes the conjugate transpose of [math]\displaystyle{ L }[/math].
The feature is optimized for performance and can handle large matrices efficiently using [math]\displaystyle{ O(n^3) }[/math] computational complexity in the worst case. It checks if the input matrix is indeed positive-definite and Hermitian before performing the decomposition and raises an error if the matrix does not meet these conditions. The feature belong to the PSD Decomposition Method feature group.
Scripting
The feature can be used from the python console as follows:
import WindLab
import GeneralToolsGui
import WindLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
def compute():
installResuslt = WindLab.installPlugin("WindLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create WindLab simulation called "Simulation"
sim = WindLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation sucessfully created
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Cholesky Decomposition"
featureGroup = "Spectrum Decomposition Method"
# create the feature
decomposedPSD = WindLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not decomposedPSD :
LabRPS.Console.PrintError("Error on creating the spectrum decomposition method.\n")
return None
# get the active simulation points feature and compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# use a vector to represent a simulation point based on its coordinates
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
v2 = vec(simPoints[1][1], simPoints[1][2], simPoints[1][3])
v3 = vec(simPoints[2][1], simPoints[2][2], simPoints[2][3])
# This feature is used to decompose power spectrum matrices which may vary in time. Let's assume that
# the active power spectrun density function in this example is stationary. Meanning it is not varying in time.
#Then, we use time instant of 0 second.
time = 0.0
# compute the decomposed cross spectrum between points 1 and 3, at time instant of 0 second and for all frequency
# increments. Note that when the following code is run, WindLab will try to identify the active frequency distribution,
# the active power spectrum feature, the active coherence function feature and others. If WindLab fails to find any
# of these dependency features, the computation will fails and specific error messages will be sent to the report view.
psd13 = sim.computeDecomposedCrossSpectrumVectorF(v1, v3, time)
# psd13 can be converted to numpy vector and be used for some other purposes.
arr = numpy.asarray(psd13)
compute()