Plugin SeaLab: Difference between revisions
| (23 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
|Version=1.0 | |Version=1.0 | ||
|Date=2024-04-15 | |Date=2024-04-15 | ||
|Features= | |Features= [[#Grid_Points|Grid Points]], [[#General_Distribution|General Distribution]], [[#Import_Simulation_Points_from_File|Import Simulation Points from File]], [[#Uniform_Random_Phases|Uniform Random Phases]], [[#Uniform_Random_Phases_Import|Uniform Random Phases Import]], [[#Double_Index_Frequency_Discretization|Double Index Frequency Discretization]], [[#Single_Index_Frequency_Discretization|Single Index Frequency Discretization]], [[#Zerva_Frequency_Discretization|Zerva Frequency Discretization]], [[#Cholesky_Decomposition|Cholesky Decomposition]], [[#Pierson_Moskowitz_Spectrum_1964|Pierson Moskowitz Spectrum (1964)]], [[#Jonswap_Spectrum_1974|Jonswap Spectrum (1974)]], [[#Gaussian_Swell_Spectrum|Gaussian Swell Spectrum]], [[#Ochi_Hubble_Spectrum|Ochi-Hubble Spectrum]], [[#Torsethaugen_Spectrum|Torsethaugen Spectrum]],[[#Bretschneider_Spectrum|Bretschneider Spectrum]], [[#ISSC_Spectrum|ISSC Spectrum]], [[#ITTC_Spectrum|ITTC Spectrum]], [[#Scott_Spectrum|Scott Spectrum]], [[#WEN_Spectrum|WEN Spectrum]], [[#Borgman_Directional_Spreading_Function|Borgman Directional Spreading Function]], [[#Cos2s_Directional_Spreading_Function|Cos2s Directional Spreading Function]], [[#Cosine_Squared_Directional_Spreading_Function|Cosine Squared Directional Spreading Function]], [[#Mitsuyasu_Directional_Spreading_Function|Mitsuyasu Directional Spreading Function]], [[#Hasselmann_Directional_Spreading_Function|Hasselmann Directional Spreading Function]], [[#Longuet_Higgins_Directional_Spreading_Function|Longuet-Higgins Directional Spreading Function]], [[#OrcaFlex_Directional_Spreading_Function|OrcaFlex Directional Spreading Function]], [[#SWOP_Directional_Spreading_Function|SWOP Directional Spreading Function]] | ||
| Line 12: | Line 12: | ||
You can find the source code of this plugin on the following Github repository: [https://github.com/LabRPS/LabRPS-plugins/tree/master/SeaLab/SeaLabPlugin Get the code here!]. This plugin is one of the official plugins provided by LabRPS. It provides very useful features (tools) for the simulation of random sea elevations. Plugins are very easy to create in LabRPS, therefore, anyone can develop plugin for any random phenomenon in LabRPS. Go to this [[Plugin_Creation|page]] to see how to create new plugin for LabRPS. You can get quick assistance from LabRPS community by sending your concern to the [https://labrps.com/boards community forum]. | You can find the source code of this plugin on the following Github repository: [https://github.com/LabRPS/LabRPS-plugins/tree/master/SeaLab/SeaLabPlugin Get the code here!]. This plugin is one of the official plugins provided by LabRPS. It provides very useful features (tools) for the simulation of random sea elevations. Plugins are very easy to create in LabRPS, therefore, anyone can develop plugin for any random phenomenon in LabRPS. Go to this [[Plugin_Creation|page]] to see how to create new plugin for LabRPS. You can get quick assistance from LabRPS community by sending your concern to the [https://labrps.com/boards community forum]. | ||
== | == Grid Points == | ||
This feature | This feature allows users to generate a set of grid points within a 3D spatial domain, ensuring that the points are evenly distributed in a plane parallel to one of the coordinate system planes (XY Plane, YZ Plane, XZ Plane). | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|Spacing1}}: This is the points spacing along one of the axis forming the plane. | ||
* {{PropertyData| | * {{PropertyData|Spacing2}}: This is the points spacing along the second axis. | ||
* {{PropertyData|Length1}}: This is the length within points are distributed along one of the axis forming the plane. | |||
* {{PropertyData|Length2}}: This is the length within points are distributed along the second axis. | |||
* {{PropertyData|CenterPoint}}: This is the center of the grid around which the points are generated. It is a 3D point. | |||
* {{PropertyData|NumberOfPoints}}: This is the resulting total number of points in the grid. This is a read only property for internal use. User cannot change its value directly. | |||
=== Scripting === | === Scripting === | ||
The following script shows how this feature can be created and used. | |||
{{Code|code= | {{Code|code= | ||
| Line 32: | Line 34: | ||
import SeaLabObjects | import SeaLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import LabRPS | |||
import numpy | import numpy | ||
import | import matplotlib.pyplot as plt | ||
from mpl_toolkits.mplot3d import Axes3D | |||
def compute(): | def compute(): | ||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
if not | # check if the simulation does really exist | ||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Grid Points" | |||
featureType = " | |||
featureGroup = "Location Distribution" | featureGroup = "Location Distribution" | ||
# create the feature | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | |||
unifSimPoints= SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not unifSimPoints: | ||
LabRPS.Console.PrintError("Error on creating the feature.\n") | LabRPS.Console.PrintError("Error on creating the uniform points feature.\n") | ||
return None | return None | ||
# | # set the plan the points grid is parallel to | ||
unifSimPoints.LocationPlan= 'YZ Plane' | |||
# let's set the | # let's set the center point of the distribution (x =0, y = 0, z = 0) | ||
unifSimPoints.CenterPoint = vec(0,0,0) | |||
# | # let's set the spacing1 (s1 = 10m) | ||
unifSimPoints.Spacing1 = '10m' | |||
# | # let's set the spacing2 (s2 = 10m) | ||
unifSimPoints.Spacing2 = '10m' | |||
# | # let's set the length1 (l1 = 200m) | ||
unifSimPoints.Length1= '200m' | |||
# let's set the length2 (l2 = 200m) | |||
unifSimPoints.Length2= '200m' | |||
# compute the simulation points coordinates. SeaLab will internally use the "unifSimPoints" feature. | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
= | # now you can convert the coordinate matrix to numpy array and use it for any other purposes | ||
arr = numpy.asarray(simPoints) | |||
# Example 3D points | |||
x = arr[:,1] | |||
y = arr[:,2] | |||
z = arr[:,3] | |||
# you can also show the result in a table, pass False as last argument to the function to ask | |||
# LabRPS to only show the data without plotting them | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False) | |||
# Create a figure | |||
fig = plt.figure() | |||
== | # Add 3D axes | ||
ax = fig.add_subplot(111, projection='3d') | |||
# Plot points | |||
ax.scatter(x, y, z, color='blue') | |||
# Hide all axes and labels | |||
ax.set_axis_off() | |||
{{Code|code= | # Set the title | ||
ax.set_title('3D Plotting of Points') | |||
# Show the plot | |||
plt.show() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== General Distribution == | |||
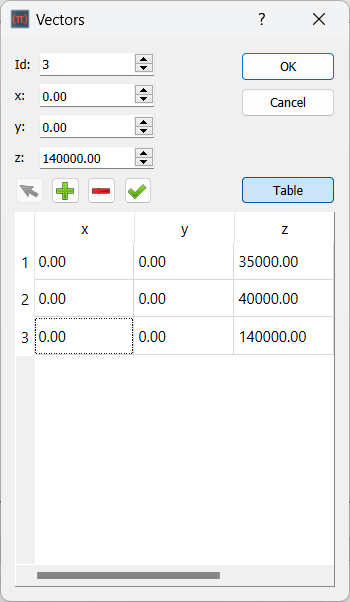
When the simulation points distribution is more general and does not follow any of the previous uniform distribution, this feature can be used. This feature allows users to input simulation points one by one using their coordinates based on the vector dialog shown below: | |||
[[Image:WindLab_Tutorial001_Pic005_WindLab_Feat_Locations_2.png|400px]] | |||
=== Properties === | |||
* {{PropertyData|Locations}}: This is a list holding the simulation points | |||
=== Scripting === | |||
The following script shows how this feature can be created and used. | |||
{{Code|code= | |||
import SeaLab | import SeaLab | ||
import GeneralToolsGui | import GeneralToolsGui | ||
import SeaLabObjects | import SeaLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import LabRPS | |||
import numpy | import numpy | ||
def compute(): | def compute(): | ||
| Line 114: | Line 147: | ||
# create SeaLab simulation called "Simulation" | # create SeaLab simulation called "Simulation" | ||
sim = SeaLabObjects.makeSimulation(doc, "Simulation") | sim = SeaLabObjects.makeSimulation(doc, "Simulation") | ||
# check if the simulation | # check if the simulation does really exist | ||
if not sim: | if not sim: | ||
LabRPS.Console.PrintError("The simulation does not exist.\n") | LabRPS.Console.PrintError("The simulation does not exist.\n") | ||
return None | return None | ||
featureType = " | featureType = "General Distribution" | ||
featureGroup = "Location Distribution" | featureGroup = "Location Distribution" | ||
# create the feature | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | |||
genSimPoints= SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not genSimPoints: | ||
LabRPS.Console.PrintError("Error on creating the feature.\n") | LabRPS.Console.PrintError("Error on creating the uniform points feature.\n") | ||
return None | return None | ||
# | # create the simulation points by their coordinates | ||
v1 = vec(0, 0, 35000) | |||
v2 = vec(0, 0, 40000) | |||
v3 = vec(0, 0, 140000) | |||
# | # add the points to the locations | ||
genSimPoints.Locations = [v1, v2, v3] | |||
# compute the simulation points coordinates. SeaLab will internally use the " | # compute the simulation points coordinates. SeaLab will internally use the "genSimPoints" feature | ||
simPoints = sim.computeLocationCoordinateMatrixP3() | simPoints = sim.computeLocationCoordinateMatrixP3() | ||
| Line 152: | Line 188: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Import Simulation Points from File == | ||
When the simulation points are stored in a file, this feature can be used. The feature allows users to import simulation points coordinates from file. Note that, for now only tab separated text file is supported and the file is expected to have number of rows and number of columns which are number of simulation points and four, respectively. | |||
[[Image:SeaLab_Tutorial001_Pic006_SeaLab_Feat_Locations_1.png|400px]] | |||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|FilePath}}: This is the path to the file. | ||
=== Scripting === | === Scripting === | ||
The following script shows how this feature can be created and used. | |||
{{Code|code= | {{Code|code= | ||
| Line 175: | Line 207: | ||
import SeaLabObjects | import SeaLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import LabRPS | |||
import numpy | import numpy | ||
def compute(): | def compute(): | ||
| Line 190: | Line 222: | ||
# check if the simulation does really exist | # check if the simulation does really exist | ||
if not sim: | if not sim: | ||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = " | featureType = "Import Simulation Points from File" | ||
featureGroup = "Location Distribution" | featureGroup = "Location Distribution" | ||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | # case you don't understand the next line) | ||
simPoints= SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not simPoints: | ||
LabRPS.Console.PrintError("Error on creating the simulation points feature.\n") | |||
return None | |||
# set the direction of the distribution to be vertical | # set the direction of the distribution to be vertical | ||
simPoints.FilePath = "D:/Points.txt" | |||
# compute the simulation points coordinates. SeaLab will internally use the "simPoints" feature. | |||
importedSimPoints = sim.computeLocationCoordinateMatrixP3() | |||
# compute the simulation points coordinates. SeaLab will internally use the " | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | # now you can convert the coordinate matrix to numpy array and use it for any other purposes | ||
arr = numpy.asarray( | arr = numpy.asarray(importedSimPoints ) | ||
# you can also show the result in a table, pass False as last argument to the function to ask | # you can also show the result in a table, pass False as last argument to the function to ask | ||
# LabRPS to only show the data without plotting them | # LabRPS to only show the data without plotting them | ||
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, | GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, importedSimPoints, False) | ||
compute() | compute() | ||
}} | }} | ||
[[#top| Back to the Top ]] | |||
== | == Uniform Random Phases == | ||
In the simulation of random sea elevations, one common technique is to represent the random sea elevations as a sum of multiple sinusoidal components in the frequency domain. Each of these components is associated with a random phase, which determines the position of the sine wave relative to time. By assigning uniform random phases to each frequency component, the resulting time series will have random characteristics, while still adhering to the desired spectral properties, such as a specific power spectral density (PSD) or turbulence spectrum. The feature generate <math>n</math> sequences <math>(\phi_{1l}, \phi_{2l}, \phi_{3l},..., \phi_{nl}; l = 1, 2, 3, ..., N)</math> of independent random phase angles | |||
uniformly distributed over the interval <math>[0, 2\pi]</math> by default. | |||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|MinimumValue}}: The minimum value that can be generated | ||
* {{PropertyData|MaximumValue}}: The maximum value that can be generated | |||
* {{PropertyData| | |||
=== Scripting === | === Scripting === | ||
| Line 249: | Line 272: | ||
{{Code|code= | {{Code|code= | ||
import SeaLab | import SeaLab | ||
import SeaLabObjects | import SeaLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import numpy | import numpy | ||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = "Uniform Random Phases" | |||
featureGroup = "Randomness Provider" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
randomness = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not randomness: | |||
LabRPS.Console.PrintError("Error on creating the randomness feature.\n") | |||
# abord the computation | |||
randomness.MinimumValue = 0 | |||
randomness.MaximumValue = 6.28 | |||
# generate random phase angle | |||
randomnessMatrix = sim.generateRandomMatrixFP() | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | |||
arr = numpy.asarray(randomnessMatrix) | |||
}} | |||
[[#top| Back to the Top ]] | |||
== Uniform Random Phases Import == | |||
When the simulation numbers are stored in a file, this feature can be used. The feature allows users to import random numbers from file. Note that, for now only tab separated text file is supported and the file is expected to have number of rows and number of columns which are number of frequency increments and number of simulation points, respectively. | |||
=== Properties === | |||
* {{PropertyData|FilePath}}: This is the path to the file. | |||
=== Scripting === | |||
The following script shows how this feature can be created and used. | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
from LabRPS import Vector as vec | |||
import numpy | |||
# | # get an existing SeaLab simulation called "Simulation" | ||
sim = SeaLab.getSimulation("Simulation") | |||
# | # check if the simulation does really exist | ||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = "Uniform Random Phases Import" | |||
featureGroup = "Randomness Provider" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
randomness = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not randomness: | |||
LabRPS.Console.PrintError("Error on creating the randomness feature.\n") | |||
# abord the computation | |||
randomness.FilePath = "myfolderpath/myfile.txt" | |||
# generate random phase angle | |||
randomnessMatrix = sim.generateRandomMatrixFP() | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | |||
arr = numpy.asarray(randomnessMatrix) | |||
}} | }} | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Single Index Frequency Discretization == | ||
This feature allows to discretize continuous frequency according to the following formula: | |||
<math>\omega_{l} = l\Delta\omega; \quad l = 1, 2, 3, ..., N</math>. | |||
* | where: | ||
* <math>\Delta\omega</math> is the frequency increment, | |||
* <math>N</math> is the number of frequency increments, | |||
=== Scripting === | === Scripting === | ||
| Line 350: | Line 375: | ||
{{Code|code= | {{Code|code= | ||
import SeaLab | import SeaLab | ||
import SeaLabObjects | import SeaLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import numpy | import numpy | ||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = "Single Index Frequency Discretization" | |||
featureGroup = "Frequency Distribution" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
frequency = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not frequency: | |||
LabRPS.Console.PrintError("Error on creating the frequency feature.\n") | |||
# abord the computation | |||
# compute the freqency distribution | |||
frequencyMatrix = sim.computeFrequenciesMatrixFP() | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | |||
arr = numpy.asarray(frequencyMatrix) | |||
}} | }} | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Double Index Frequency Discretization == | ||
This feature allows to discretize continuous frequency according to the following formula: | |||
<math>\omega_{ml} = (l-1)\Delta\omega + \frac{m}{n}\Delta\omega; \quad m = 1, 2, 3, ..., n; \quad l = 1, 2, 3, ..., N</math>. | |||
* | where: | ||
* <math>\Delta\omega</math> is the frequency increment, | |||
* <math>n</math> is the number of simulation points, | |||
* <math>N</math> is the number of frequency increments, | |||
=== Scripting === | === Scripting === | ||
| Line 422: | Line 427: | ||
{{Code|code= | {{Code|code= | ||
import SeaLab | import SeaLab | ||
import SeaLabObjects | import SeaLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import numpy | import numpy | ||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
# abord the computation | |||
featureType = "Double Index Frequency Discretization" | |||
featureGroup = "Frequency Distribution" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
frequency = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not frequency: | |||
LabRPS.Console.PrintError("Error on creating the frequency feature.\n") | |||
# abord the computation | |||
# compute the freqency distribution | |||
frequencyMatrix = sim.computeFrequenciesMatrixFP() | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | |||
arr = numpy.asarray(frequencyMatrix) | |||
}} | }} | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== Zerva Frequency Discretization == | |||
This feature allow to discretize continuous frequency according to the following formula: | |||
<math>\omega_{l} = (1+\frac{l}{2})\Delta\omega;\quad l = 1, 2, 3, ..., N</math>, | |||
* | where: | ||
* | * <math>\Delta\omega</math> is the frequency increment, | ||
* <math>N</math> is the number of frequency increments, | |||
=== Scripting === | === Scripting === | ||
| Line 502: | Line 490: | ||
# abord the computation | # abord the computation | ||
featureType = " | featureType = "Zerva Frequency Discretization" | ||
featureGroup = " | featureGroup = "Frequency Distribution" | ||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | # case you don't understand the next line) | ||
frequency = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not frequency: | ||
LabRPS.Console.PrintError("Error on creating the | LabRPS.Console.PrintError("Error on creating the frequency feature.\n") | ||
# abord the computation | # abord the computation | ||
# compute the freqency distribution | |||
frequencyMatrix = sim.computeFrequenciesMatrixFP() | |||
# | |||
# now you can convert the coordinate matrix to numpy array and use it for any other purposes | # now you can convert the coordinate matrix to numpy array and use it for any other purposes | ||
arr = numpy.asarray( | arr = numpy.asarray(frequencyMatrix) | ||
}} | }} | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Cholesky Decomposition == | ||
This feature performs the [https://en.wikipedia.org/wiki/Cholesky_decomposition Cholesky decomposition] of a positive Hermitian power spectrum matrix and returns the lower triangular matrix (L) of the decomposition. The Cholesky decomposition is a numerical method used to decompose a positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. Specifically, for a matrix | |||
A, the decomposition is given by: | |||
<math display=block>\mathbf{A} = \mathbf{L L}^{*},</math> | |||
<math display=block> L_{j,j} = \sqrt{ A_{j,j} - \sum_{k=1}^{j-1} L_{j,k}^*L_{j,k} }, </math> | |||
<math display=block> L_{i,j} = \frac{1}{L_{j,j}} \left( A_{i,j} - \sum_{k=1}^{j-1} L_{j,k}^* L_{i,k} \right) \quad \text{for } i>j. </math> | |||
where <math>L</math> is a [https://en.wikipedia.org/wiki/Triangular_matrix lower triangular matrix] with real and positive diagonal entries, and <math>L^*</math> denotes the [https://en.wikipedia.org/wiki/Conjugate_transpose conjugate transpose] of <math>L</math>. | |||
The feature is optimized for performance and can handle large matrices efficiently using <math>O(n^3)</math> computational complexity in the worst case. It checks if the input matrix is indeed positive-definite and Hermitian before performing the decomposition and raises an error if the matrix does not meet these conditions. The feature belong to the [[RPS_Feature_Group#PSD_Decomposition_Method|PSD Decomposition Method]] feature group. | |||
=== | === Feature Dependency === | ||
The features required by this feature are summarized as follows: | |||
* | * A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | ||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
* A [[SeaLab_Feature#Spectrum| spectrum feature]] | |||
=== Scripting === | === Scripting === | ||
The | The feature can be used from the python console as follows: | ||
{{Code|code= | {{Code|code= | ||
import SeaLab | import SeaLab | ||
import GeneralToolsGui | |||
import SeaLabObjects | import SeaLabObjects | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
import LabRPS | |||
import numpy | import numpy | ||
def compute(): | |||
installResuslt = SeaLab.installPlugin("SeaLabPlugin") | |||
doc = LabRPS.ActiveDocument | |||
if not doc: | |||
doc = LabRPS.newDocument() | |||
# create SeaLab simulation called "Simulation" | |||
sim = SeaLabObjects.makeSimulation(doc, "Simulation") | |||
# check if the simulation sucessfully created | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Cholesky Decomposition" | |||
featureGroup = "Spectrum Decomposition Method" | |||
# create the feature | |||
decomposedPSD = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not decomposedPSD : | |||
LabRPS.Console.PrintError("Error on creating the spectrum decomposition method.\n") | |||
return None | |||
# get the active simulation points feature and compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n") | |||
return None | |||
# use a vector to represent a simulation point based on its coordinates | |||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
v2 = vec(simPoints[1][1], simPoints[1][2], simPoints[1][3]) | |||
v3 = vec(simPoints[2][1], simPoints[2][2], simPoints[2][3]) | |||
# This feature is used to decompose power spectrum matrices which may vary in time. Let's assume that | |||
# the active power spectrun density function in this example is stationary. Meanning it is not varying in time. | |||
#Then, we use time instant of 0 second. | |||
time = 0.0 | |||
}} | # compute the decomposed cross spectrum between points 1 and 3, at time instant of 0 second and for all frequency | ||
# increments. Note that when the following code is run, SeaLab will try to identify the active frequency distribution, | |||
# the active power spectrum feature, the active coherence function feature and others. If SeaLab fails to find any | |||
# of these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
psd13 = sim.computeDecomposedCrossSpectrumVectorF(v1, v3, time) | |||
# psd13 can be converted to numpy vector and be used for some other purposes. | |||
arr = numpy.asarray(psd13) | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Pierson Moskowitz Spectrum 1964 == | ||
Various idealized spectra are used to answer the question in oceanography and ocean engineering. Perhaps the simplest is that proposed by Pierson and Moskowitz 1964. They assumed that if the wind blew steadily for a long time over a large area, the waves would come into equilibrium with the wind. This is the concept of a fully developed sea (a sea produced by winds blowing steadily over hundreds of miles for several days).Here, a long time is roughly ten-thousand wave periods, and a "large area" is roughly five-thousand wave-lengths on a side. ([https://wikiwaves.org/Ocean-Wave_Spectra#Pierson-Moskowitz_Spectrum source]): | |||
<math>S(\omega) = \frac{5}{16}H^2_s\omega^4_p\omega^{-5}\mbox{exp}\left [ -\frac{5}{4}\left ( \frac{\omega}{\omega_p} \right )^{-4} \right ]</math> | |||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
* {{PropertyData|SignificantWaveHeight}}: The significant wave height. | |||
* | * {{PropertyData|PeakPeriod}}: The peak period. | ||
=== Scripting === | === Scripting === | ||
The | The feature can be used from the python console as follows: | ||
{{Code|code= | {{Code|code= | ||
import SeaLab | import SeaLab | ||
import SeaLabObjects | import SeaLabObjects | ||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Pierson Moskowitz Spectrum (1964)" | |||
featureGroup = "Frequency Spectrum" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not spectrum: | |||
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n") | |||
return None | |||
sim.MaxFrequency = '0.04 1/s' | |||
sim.NumberOfFrequency = 1024 | |||
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency | |||
sim.setActiveFeature(spectrum) | |||
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s. | |||
time = 0.0 | |||
# compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n") | |||
return None | |||
== | # let pick the first simulation point | ||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
# compute the spectrum vector at time instant of 0 second | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time) | |||
# show the results | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== Jonswap Spectrum 1974 == | |||
Hasselmann et al. 1973, after analyzing data collected during the Joint North Sea Wave Observation Project JONSWAP, found that the wave spectrum is never fully developed. It continues to develop through non-linear, wave-wave interactions even for very long times and distances. Hence an extra and somewhat artificial factor was added to the Pierson-Moskowitz spectrum in order to improve the fit to their measurements. The JONSWAP spectrum is thus a Pierson-Moskowitz spectrum multiplied by an extra peak enhancement factor <math>\gamma ^r</math> ([https://wikiwaves.org/Ocean-Wave_Spectra#JONSWAP_Spectrum source]): | |||
<math>S(\omega) = \frac{5}{16}A_{\gamma}H^2_s\omega^4_p\omega^{-5}\mbox{exp}\left [ -\frac{5}{4}\left ( \frac{\omega}{\omega_p} \right )^{-4} \right ]\gamma^r </math> | |||
where: | where: | ||
= | <math>A_{\gamma} = 1 - 0.287 \times ln\left ( \gamma \right ) \quad \mbox{is a normalizing factor} </math> | ||
<math>r = \mbox{exp}\left [ -\frac{1}{2}\left ( \frac{\omega-\omega_p}{\sigma\omega_p} \right )^{2} \right ]</math> | |||
<math>\sigma = | |||
\begin{cases} | |||
\sigma_1, & \mbox{for } \omega \le \omega_p \\ | |||
\\ | |||
\sigma_2, & \mbox{for } \omega > \omega_p | |||
\end{cases} | |||
</math> | |||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
}} | * {{PropertyData|SignificantWaveHeight}}: The significant wave height. | ||
* {{PropertyData|PeakPeriod}}: The peak period. | |||
* {{PropertyData|AutoGamma}}: Whether to automatically compute gamma or not. | |||
* {{PropertyData|AutoSigma}}: Whether to automatically compute sigma or not. | |||
* {{PropertyData|Gamma}}: The value of shape parameter gamma. | |||
* {{PropertyData|Sigma1}}: The width of spectral peak sigma 1. | |||
* {{PropertyData|Sigma2}}: The width of spectral peak sigam 2. | |||
* | |||
* | |||
=== Scripting === | === Scripting === | ||
The | The feature can be used from the python console as follows: | ||
{{Code|code= | {{Code|code= | ||
import SeaLab | import SeaLab | ||
import SeaLabObjects | import SeaLabObjects | ||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Jonswap Spectrum (1974)" | |||
featureGroup = "Frequency Spectrum" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not spectrum: | |||
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n") | |||
return None | |||
sim.MaxFrequency = '0.04 1/s' | |||
sim.NumberOfFrequency = 1024 | |||
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency | |||
sim.setActiveFeature(spectrum) | |||
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s. | |||
time = 0.0 | |||
# compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n") | |||
return None | |||
== | # let pick the first simulation point | ||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
# compute the spectrum vector at time instant of 0 second | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time) | |||
# show the results | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== Gaussian Swell Spectrum == | |||
The Gaussian swell spectrum is based on the normal (or Gaussian) probability density function and is defined as ([https://www.orcina.com/webhelp/OrcaFlex/Content/html/Waves,Wavespectra.htm source]): | |||
<math>S(\omega) = \left ( \frac{H_c}{4} \right )^2\frac{1}{\sigma\sqrt{2\pi}}\mbox{exp}\left [ -\frac{\left ( \omega -\omega_p \right )^2}{2\sigma^2} \right ]</math> | |||
<math | |||
=== Feature Dependency === | === Feature Dependency === | ||
| Line 752: | Line 799: | ||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | * A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | ||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | * A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | ||
=== | === Properties === | ||
The feature can be used from the python console as follows: | * {{PropertyData|SignificantWaveHeight}}: The significant wave height. | ||
* {{PropertyData|PeakFrequency}}: The peak frequency. | |||
* {{PropertyData|Sigma}}: The width of spectral peak sigma. | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | {{Code|code= | ||
import SeaLab | import SeaLab | ||
import SeaLabObjects | |||
import GeneralToolsGui | import GeneralToolsGui | ||
import | import LabRPS | ||
from LabRPS import Vector as vec | from LabRPS import Vector as vec | ||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | def compute(): | ||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
# | |||
sim = | |||
# check if the simulation | |||
if not sim: | if not sim: | ||
LabRPS.Console.PrintError("The simulation does not exist.\n") | LabRPS.Console.PrintError("The simulation does not exist.\n") | ||
return None | return None | ||
featureType = " | featureType = "Gaussian Swell Spectrum" | ||
featureGroup = "Spectrum | featureGroup = "Frequency Spectrum" | ||
# create the feature | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | |||
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not spectrum: | ||
LabRPS.Console.PrintError("Error on creating the spectrum | LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n") | ||
return None | return None | ||
# | sim.MaxFrequency = '0.04 1/s' | ||
sim.NumberOfFrequency = 1024 | |||
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency | |||
sim.setActiveFeature(spectrum) | |||
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s. | |||
time = 0.0 | |||
# compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | simPoints = sim.computeLocationCoordinateMatrixP3() | ||
| Line 799: | Line 856: | ||
return None | return None | ||
# | # let pick the first simulation point | ||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | ||
# compute the spectrum vector at time instant of 0 second | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time) | |||
# | # show the results | ||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | compute() | ||
| Line 822: | Line 871: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Ochi Hubble Spectrum == | ||
The Ochi-Hubble spectrum allows double-peaked spectra to be set up, enabling you to represent sea states that include both a remotely generated swell and a local wind generated sea. See the Ochi-Hubble paper for full details. ([https://www.orcina.com/webhelp/OrcaFlex/Content/html/Waves,Wavespectra.htm source]): | |||
<math>S(\omega) = \frac{ | <math>S(\omega) = \sum_{j=1}^2 \left\{ \frac{\left(\frac{4\lambda_j+1}{4}\right)^{\lambda_j} \omega_{\mathrm{m}_j}^{4\lambda_j}H_{\mathrm{s}_j}^2}{4\Gamma(\lambda_j)} \right\} | ||
\omega^{-(4\lambda_j+1)} | |||
\exp\left\{ -\left(\frac{4\lambda_j+1}{4}\right) \left(\frac{\omega}{\omega_{\mathrm{m}_j}}\right)^{-4} \right\} </math> | |||
where: | |||
=== Feature Dependency === | === Feature Dependency === | ||
| Line 836: | Line 889: | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|PeakShape1}}: The peak shape of the first peak. | ||
* {{PropertyData| | * {{PropertyData|PeakShape2}}: The peak shape of the second peak. | ||
* {{PropertyData|PeakFrequency1}}: The peak frequency of the first peak. | |||
* {{PropertyData|PeakFrequency2}}: The peak frequency of the second peak. | |||
* {{PropertyData|SignificantWaveHeight1}}: The significant wave height of the first peak. | |||
* {{PropertyData|SignificantWaveHeight2}}: The significant wave height of the second peak. | |||
* {{PropertyData|AutoPara}}: Whether to automatically compute the six previous parameter. | |||
* {{PropertyData|SignificantWaveHeight}}: The significant wave height used the calculate those six parameters in case of automatic parameters calculation . | |||
=== Scripting === | === Scripting === | ||
| Line 862: | Line 921: | ||
return None | return None | ||
featureType = " | featureType = "Ochi-Hubble spectrum" | ||
featureGroup = "Frequency Spectrum" | featureGroup = "Frequency Spectrum" | ||
| Line 904: | Line 963: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Torsethaugen Spectrum == | ||
The Torsethaugen spectrum is another two-peaked spectrum, more suited to North Sea application than Ochi-Hubble. The spectrum is defined by two user input parameters, <math>H_s</math> and <math>T_p (= 1/f_m)</math>. In order to define the spectrum we must first define a number of other terms ([https://www.orcina.com/webhelp/OrcaFlex/Content/html/Waves,Wavespectra.htm source]): | |||
<math> | <math> | ||
\begin{array}{lcl} | |||
a_1 = 0.5 \\ | |||
a_2 = 0.3 \\ | |||
a_3 = 6 \\ | |||
a_{10} = 0.7 \\ | |||
a_{20} = 0.6 \\ | |||
b_1 = 2\ \textrm{s} \\ | |||
G_0 = 3.26 \\ | |||
k_g = 35 \\ | |||
k_1 = 0.0016 \\ | |||
k_2 = 0.286 \\ | |||
k_3 = \frac{k_2}{k_1^{1/3}} \\ | |||
k_f = k_3 g^{-1/2} \\ | |||
F_e = 370,000\ \textrm{m} \\ | |||
a_f = k_f F_e^{1/6} \\ | |||
T_{pf} = a_f H_s^{1/3} \\ | |||
a_e = 2\ \textrm{sm}^{-1/2} \\ | |||
T_l = a_e H_s^{1/2} \\ | |||
T_u = 25\ \textrm{s} \\ | |||
\epsilon_l = \frac{T_{pf} - T_p}{T_{pf} - T_l} \\ | |||
\epsilon_u = \frac{T_p - T_{pf}}{T_u - T_{pf}} \\ | |||
\end{array} | |||
</math> | |||
Note: | |||
<math> \mbox{If }\epsilon_l < 0 \mbox{ then } \epsilon_l \mbox{ is set to 0. If } \epsilon_l > 1 \mbox{ then } \epsilon_l \mbox{ is set to 1. Likewise for } \epsilon_u.\\</math> | |||
<math> | For wind dominated sea, <math>T_p \le T_{pf}</math>, we define: | ||
<math> | |||
<math>\ | \begin{array}{lcl} | ||
\ | R_w = (1 - a_{10}) \exp\{-(\epsilon_l/a_1)^2\} + a_{10} \\ | ||
\ | H_1 = R_w H_s \\ | ||
\\ | T_{p1} = T_p \\ | ||
\ | s_p = \frac{2\pi}{g}\frac{H_1}{T_{p1}^2} \\ | ||
\end{ | \gamma = k_g s_p^{6/7} \\ | ||
H_2 = (1 - R_w^2)^{1/2} H_s \\ | |||
T_{p2} = T_{pf} + b_1 \\ | |||
\end{array} | |||
</math> | </math> | ||
For swell dominated sea, <math>T_p > T_{pf}</math>, we define: | |||
=== | <math> | ||
\begin{array}{lcl} | |||
R_s = (1 - a_{20}) \exp(-(\epsilon_u/a_2)^2) + a_{20} \\ | |||
H_1 = R_s H_s \\ | |||
T_{p1} = T_p \\ | |||
s_f = \frac{2\pi}{g}\frac{H_s}{T_{pf}^2} \\ | |||
\gamma_f = k_g s_f^{6/7} \\ | |||
\gamma = \gamma_f (1 + a_3 \epsilon_u) \\ | |||
H_2 = (1 - R_s^2)^{1/2} H_s \\ | |||
T_{p2} = a_f H_2^{1/3} \\ | |||
\end{array} | |||
</math> | |||
Note: | |||
If <math>\gamma < 1</math> then <math>\gamma</math> is set to 1. | |||
These two branches of the formulation define <math>H_1, H_2, T_{p1}, T_{p2}</math> and <math>\gamma</math> which are then used to define the spectrum as | |||
<math>S(f) = \sum_{j=1}^2 E_j S_{jn}(f_{jn})</math> | |||
where: | |||
<math> | |||
\begin{array}{lcl} | |||
j = 1\ \textrm{is the primary sea system} \\ | |||
j = 2\ \textrm{is the secondary sea system} \\ | |||
f_{1n} = f T_{p1} \\ | |||
f_{2n} = f T_{p2} \\ | |||
\sigma = | |||
\begin{cases} | |||
0.07 \quad \mbox{for } f_{1n} \le 1 \\ | |||
0.09 \quad \mbox{for } f_{1n} \gt 1 \\ | |||
\end{cases} \\ | |||
E_1 = (1/16) H_1^2 T_{p1} \\ | |||
E_2 = (1/16) H_2^2 T_{p2} \\ | |||
A_\gamma = \frac{1 + 1.1 \log_e(\gamma)^{1.19}}{\gamma} \\ | |||
S_{1n}(f_{1n}) = G_0 A_\gamma f_{1n}^{-4} \exp(-f_{1n}^{-4}) \gamma^{\exp\{-(1/2\sigma^2) (f_{1n} - 1)^2\}} \\ | |||
S_{2n}(f_{2n}) = G_0 f_{2n}^{-4} \exp(-f_{2n}^{-4}) \\ | |||
\end{array} | |||
</math> | |||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
* {{PropertyData|SignificantWaveHeight}}: The significant wave height. | |||
* {{PropertyData|PeakPeriod}}: The peak period. | |||
* {{PropertyData|AutoGamma}}: Whether to automatically compute gamma or not. | |||
* {{PropertyData|AutoSigma}}: Whether to automatically compute sigma or not. | |||
* {{PropertyData|Gamma}}: The value of shape parameter gamma. | |||
* {{PropertyData|Sigma1}}: The width of spectral peak sigma 1. | |||
* {{PropertyData|Sigma2}}: The width of spectral peak sigam 2. | |||
* {{PropertyData|DoublePeaks}}: Whether double peaks or not. | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | |||
== | # Before you run this code, you should first have created a document with a SeaLab simulation with | ||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Torsethaugen Spectrum" | |||
featureGroup = "Frequency Spectrum" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not spectrum: | |||
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n") | |||
return None | |||
sim.MaxFrequency = '0.04 1/s' | |||
sim.NumberOfFrequency = 1024 | |||
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency | |||
sim.setActiveFeature(spectrum) | |||
= | # For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s. | ||
time = 0.0 | |||
# compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n") | |||
return None | |||
# let pick the first simulation point | |||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
# compute the spectrum vector at time instant of 0 second | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time) | |||
# show the results | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
{{Code|code= | == Bretschneider Spectrum == | ||
import SeaLab | |||
import SeaLabObjects | The Bretschneider Spectrum is a two-parameter spectral model based on the assumption that the waves are narrow-banded with the wave characteristics following the Rayleigh distribution: | ||
import GeneralToolsGui | |||
import LabRPS | <math>S(\omega) = C_1\times H^2_s\left ( \frac{\omega^4_0}{\omega^5} \right )\mbox{exp}\left [ C_2\left ( \frac{\omega_0}{\omega} \right )^2 \right ]</math> | ||
from LabRPS import Vector as vec | |||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
* {{PropertyData|SignificantWaveHeight}}: The significant wave height. | |||
* {{PropertyData|SignificantWavePeriod}}: The significant wave period defined as the average period of the significant waves. | |||
* {{PropertyData|Constant1}}: A constant (0.2107 by default). | |||
* {{PropertyData|Constant2}}: A constant (-0.8429 by default). | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | |||
# Before you run this code, you should first have created a document with a SeaLab simulation with | # Before you run this code, you should first have created a document with a SeaLab simulation with | ||
| Line 1,047: | Line 1,175: | ||
return None | return None | ||
featureType = " | featureType = "Bretschneider Spectrum" | ||
featureGroup = "Frequency Spectrum" | featureGroup = "Frequency Spectrum" | ||
| Line 1,089: | Line 1,217: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == ISSC Spectrum == | ||
The | The International Ship Structures Congress (1964) suggested slight modification of the Bretschneider spectrum given as: | ||
<math>S(\omega) = \ | <math>S(\omega) = C_1\times H^2_s\left ( \frac{\omega^4_0}{\omega^5} \right )\mbox{exp}\left [ C_2\left ( \frac{\omega_0}{\omega} \right )^2 \right ]</math> | ||
=== Feature Dependency === | === Feature Dependency === | ||
| Line 1,107: | Line 1,231: | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|SignificantWaveHeight}}: The significant wave height. | ||
* {{PropertyData|SignificantWavePeriod}}: The significant wave period defined as the average period of the significant waves. | |||
* {{PropertyData|Constant1}}: A constant (0.3123 by default). | |||
* {{PropertyData|Constant2}}: A constant (-1.2489 by default). | |||
* {{PropertyData| | |||
* {{PropertyData| | |||
* {{PropertyData| | |||
=== Scripting === | === Scripting === | ||
| Line 1,139: | Line 1,259: | ||
return None | return None | ||
featureType = " | featureType = "ISSC Spectrum" | ||
featureGroup = "Frequency Spectrum" | featureGroup = "Frequency Spectrum" | ||
| Line 1,181: | Line 1,301: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == ITTC Spectrum == | ||
The | The Pierson Moskowitz spectrum was modified in the International Towing Tank Conference (1966, 1969,1972) given as: | ||
<math> | <math>S(\omega) = \alpha g^2\omega^{-5}\mbox{exp}\left ( -\frac{4\alpha g^2\omega^{-4}}{H^2_s} \right )</math> | ||
\ | |||
</math> | |||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
* {{PropertyData|SignificantWaveHeight}}: The significant wave height. | |||
* {{PropertyData|PhillipsConstant}}:The Phillips Constant (0.0081 by default). | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | |||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "ITTC Spectrum" | |||
featureGroup = "Frequency Spectrum" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not spectrum: | |||
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n") | |||
return None | |||
sim.MaxFrequency = '0.04 1/s' | |||
sim.NumberOfFrequency = 1024 | |||
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency | |||
sim.setActiveFeature(spectrum) | |||
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s. | |||
time = 0.0 | |||
= | # compute the simulation points coordinates | ||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n") | |||
return None | |||
== | # let pick the first simulation point | ||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
# compute the spectrum vector at time instant of 0 second | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time) | |||
# show the results | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== Scott Spectrum == | |||
The Pierson Moskowitz spectrum was modified in the International Towing Tank Conference (1966, 1969,1972) given as: | |||
# Before you run this code, you should first have created a document with a SeaLab simulation with | <math>S(\omega) = 0.214 H^2_s\mbox{exp}\left [ -\frac{1}{0.065}\left ( \frac{\omega-\omega_p}{ \omega-\omega_p +0.26} \right )^{1/2} \right ], \quad \mbox{for } -0.26<\omega-\omega_p < 1.65 \mbox{ and } 0 \mbox{ elsewhere.}</math> | ||
# active simulation points and frequency distribution | |||
def compute(): | === Feature Dependency === | ||
The features required by this feature are summarized as follows: | |||
# get an existing SeaLab simulation called "Simulation" | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
* {{PropertyData|SignificantWaveHeight}}: the significant wave height. | |||
* {{PropertyData|PeakFrequency}} the peak frequency of the spectrum. | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | |||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | sim = SeaLab.getSimulation("Simulation") | ||
| Line 1,309: | Line 1,423: | ||
return None | return None | ||
featureType = " | featureType = "Scott Spectrum" | ||
featureGroup = "Frequency Spectrum" | featureGroup = "Frequency Spectrum" | ||
| Line 1,351: | Line 1,465: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == WEN Spectrum == | ||
WEN spectrum is the wave spectrum of China offshore. It can describe the different stages of wind wave growth and adapt to different water depths: | |||
<math>S(\omega) = \frac{m_0p}{\omega_w}\mbox{exp}\left \{ -95\left [ ln\frac{p \left ( 5.813− 5.137\eta \right )}{\left ( 6.77− 1.088p+0.013p^2 \right )\left ( 1.307− 1.426\eta \right )} \right ]\left ( \frac{\omega}{\omega_0} - 1\right )^{12/5} \right \}, \quad \mbox{for } 0 \le \omega \le 1.15\omega_w</math> | |||
<math>S(\omega) = | <math>S(\omega) = \frac{m_0}{\omega_w} \frac{\left ( 6.77− 1.088p+0.013p^2 \right )\left ( 1.307− 1.426\eta \right )}{ 5.813− 5.137\eta} \left ( \frac{1.15\omega_w}{\omega} \right )^m, \quad \mbox{for } \omega \ge 1.15\omega_w</math> | ||
=== Feature Dependency === | === Feature Dependency === | ||
| Line 1,365: | Line 1,482: | ||
=== Properties === | === Properties === | ||
* {{PropertyData|SignificantWaveHeight}}: | * {{PropertyData|SignificantWaveHeight}}: the significant wave height. | ||
* {{PropertyData|SignificantWavePeriod}} | * {{PropertyData|SignificantWavePeriod}} significant wave period defined as the average period of the significant waves. | ||
* {{PropertyData| | * {{PropertyData|DepthParameter}}: The depth parameter taken between 0 and 0.5. | ||
* {{PropertyData| | * {{PropertyData|TenMetersHeightMeanWindSpeed}} the mean wind speed at 10 meters above ground. | ||
=== Scripting === | === Scripting === | ||
| Line 1,393: | Line 1,510: | ||
return None | return None | ||
featureType = " | featureType = "WEN Spectrum" | ||
featureGroup = "Frequency Spectrum" | featureGroup = "Frequency Spectrum" | ||
| Line 1,405: | Line 1,522: | ||
return None | return None | ||
sim.MaxFrequency = ' | sim.MaxFrequency = '4 1/s' | ||
sim.NumberOfFrequency = 1024 | sim.NumberOfFrequency = 1024 | ||
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency | sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency | ||
| Line 1,435: | Line 1,552: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Borgman Directional Spreading Function == | ||
The Borgman directional spreading function is based on a circular normal distribution of Mobarek (1965) and Fan (1968): | |||
<math>D(\theta) = \frac{1}{2I_0\left ( \theta_p \right )}\mbox{exp}\left [ a\mbox{cos}\left ( \theta - \theta_p \right ) \right ]</math> | |||
where: | |||
<math> | <math>I_0\left ( \theta_p \right )</math> is the Bessel function of the second kind and zeroth order. | ||
=== Feature Dependency === | === Feature Dependency === | ||
| Line 1,449: | Line 1,570: | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|AngleOfPropagationOfPredominantWaveEnergy}}: The angle of propagation of predominant wave energy.. | ||
* {{PropertyData|PositiveConstant}} : A positive constant. | |||
* {{PropertyData| | |||
=== Scripting === | === Scripting === | ||
| Line 1,477: | Line 1,596: | ||
return None | return None | ||
featureType = " | featureType = "Borgman Directional Spreading Function" | ||
featureGroup = " | featureGroup = "Directional Spreading Function" | ||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | # case you don't understand the next line) | ||
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not spreading: | ||
LabRPS.Console.PrintError("Error on creating the | LabRPS.Console.PrintError("Error on creating the spreading function feature.\n") | ||
return None | return None | ||
sim. | sim.MinDirection = '-90 deg' | ||
sim. | sim.MaxDirection = '90 deg' | ||
sim. | sim.NumberOfDirectionIncrements = 1024 | ||
sim.setActiveFeature( | sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements | ||
sim.setActiveFeature(spreading) | |||
# For this example we shall compute the | # For this example we shall compute the spreading function for the frequency value of 0.25 rad/s. | ||
frequency = 0.04 #hz | |||
# compute the simulation points coordinates | # compute the simulation points coordinates | ||
| Line 1,501: | Line 1,621: | ||
if not simPoints : | if not simPoints : | ||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least | LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n") | ||
return None | return None | ||
# let pick the first simulation point | # let pick the first simulation point | ||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | ||
# compute the | # compute the spreading function vector for a frequency of 0.24 rad/s | ||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | # Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | ||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | # If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | ||
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency) | |||
# show the results | # show the results | ||
GeneralToolsGui.GeneralToolsPyTool.showArray(len( | GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings) | ||
LabRPS.ActiveDocument.recompute() | LabRPS.ActiveDocument.recompute() | ||
| Line 1,519: | Line 1,639: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Cos2s Directional Spreading Function == | ||
The | The Cos2s directional spreading function is based on the cosine function with a spreading parameter which does not vary with frequency: | ||
<math> | <math>D(\theta) = \frac{\Gamma^2\left ( s+1\right )}{\Gamma\left ( 2s+1\right )}\mbox{cos}^{2s}\left ( \frac{\theta -\theta_0}{2} \right )</math> | ||
=== Feature Dependency === | === Feature Dependency === | ||
| Line 1,533: | Line 1,653: | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|PrincipalWaveDirection}}: The angle defining the principal direction in which the wave is propagating. | ||
* {{PropertyData| | * {{PropertyData|SpreadingExponent}} :The spreading exponent. | ||
=== Scripting === | === Scripting === | ||
| Line 1,559: | Line 1,679: | ||
return None | return None | ||
featureType = " | featureType = "Cos2s Directional Spreading Function" | ||
featureGroup = " | featureGroup = "Directional Spreading Function" | ||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | # case you don't understand the next line) | ||
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not spreading: | ||
LabRPS.Console.PrintError("Error on creating the | LabRPS.Console.PrintError("Error on creating the spreading function feature.\n") | ||
return None | return None | ||
sim. | sim.MinDirection = '-90 deg' | ||
sim. | sim.MaxDirection = '90 deg' | ||
sim. | sim.NumberOfDirectionIncrements = 1024 | ||
sim.setActiveFeature( | sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements | ||
sim.setActiveFeature(spreading) | |||
# For this example we shall compute the | # For this example we shall compute the spreading function for the frequency value of 0.25 rad/s. | ||
frequency = 0.04 #hz | |||
# compute the simulation points coordinates | # compute the simulation points coordinates | ||
| Line 1,583: | Line 1,704: | ||
if not simPoints : | if not simPoints : | ||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least | LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n") | ||
return None | return None | ||
# let pick the first simulation point | # let pick the first simulation point | ||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | ||
# compute the | # compute the spreading function vector for a frequency of 0.24 rad/s | ||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | # Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | ||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | # If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | ||
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency) | |||
# show the results | # show the results | ||
GeneralToolsGui.GeneralToolsPyTool.showArray(len( | GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings) | ||
LabRPS.ActiveDocument.recompute() | LabRPS.ActiveDocument.recompute() | ||
compute() | compute() | ||
}} | }} | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == Cosine Squared Directional Spreading Function == | ||
The | The cosine squared directional spreading function assumes that spreading is proportional to <math>(cos 0)^2</math>. It does not vary with frequency: | ||
<math> | <math>D(\theta) = \left ( \frac{2}{\pi} \right )\mbox{cos}^{2}\left ( \theta \right )</math> | ||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | |||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Cosine Squared Directional Spreading Function" | |||
featureGroup = "Directional Spreading Function" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not spreading: | |||
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n") | |||
return None | |||
sim.MinDirection = '-90 deg' | |||
sim.MaxDirection = '90 deg' | |||
sim.NumberOfDirectionIncrements = 1024 | |||
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements | |||
sim.setActiveFeature(spreading) | |||
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s. | |||
frequency = 0.04 #hz | |||
# compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n") | |||
return None | |||
# let pick the first simulation point | |||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
# compute the spreading function vector for a frequency of 0.24 rad/s | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency) | |||
# show the results | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== Mitsuyasu Directional Spreading Function == | |||
Mitsuyasu et al. (1975) propose the following directional spreading function: | |||
<math>D(\theta, \omega) = \frac{2^{2s-1}}{\pi}\frac{\Gamma^2\left ( s+1\right )}{\Gamma\left ( 2s+1\right )}\left | \mbox{cos}\left ( \frac{\theta}{2} \right )\right |^{2s} </math> | |||
where: | |||
<math>s = | |||
\begin{cases} | |||
s_m\left ( \frac{\omega}{\omega_m} \right )^5, & \mbox{for } \omega \le \omega_m \\ | |||
\\ | |||
s_m\left ( \frac{\omega}{\omega_m} \right )^{-2.5}, & \mbox{for } \omega > \omega_m | |||
\end{cases} | |||
</math> | |||
<math>s_m = 11.5\left ( \frac{\omega_mU}{g} \right )^{-2.5}</math> | |||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
* {{PropertyData|ModalFrequency}}: The modal frequency. | |||
* {{PropertyData|TenMeterHeightmeanWindSpeed}} : The mean wind speed at 10 meters above aground. | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | |||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Mitsuyasu Directional Spreading Function" | |||
featureGroup = "Directional Spreading Function" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not spreading: | |||
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n") | |||
return None | |||
spreading.ModalFrequency = '0.004 1/s' | |||
sim.MinDirection = '-90 deg' | |||
sim.MaxDirection = '90 deg' | |||
sim.NumberOfDirectionIncrements = 1024 | |||
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements | |||
sim.setActiveFeature(spreading) | |||
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s. | |||
frequency = 0.004 #hz | |||
# compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n") | |||
return None | |||
# let pick the first simulation point | |||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
# compute the spreading function vector for a frequency of 0.24 rad/s | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency) | |||
# show the results | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== Hasselmann Directional Spreading Function == | |||
From analysis of measured data, Hasselmann et al. (1980) propose the following directional spreading function: | |||
<math>D(\theta, \omega) = \frac{2^{2s-1}}{\pi}\frac{\Gamma^2\left ( s+1\right )}{\Gamma\left ( 2s+1\right )}\left | \mbox{cos}\left ( \frac{\theta}{2} \right )\right |^{2s} </math> | |||
where: | |||
<math>s = | |||
\begin{cases} | |||
6.97\left ( \frac{\omega}{\omega_m} \right )^{4.06}, & \mbox{for } \omega \le 1.05\omega_m \\ | |||
\\ | |||
9.77\left ( \frac{\omega}{\omega_m} \right )^{\mu}, & \mbox{for } \omega > 1.05\omega_m | |||
\end{cases} | |||
</math> | |||
<math>s_m = -2.33-1.45\left ( \frac{\omega_mU}{g} -1.17\right )</math> | |||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
* {{PropertyData|ModalFrequency}}: The modal frequency. | |||
* {{PropertyData|MeanWindSpeed}} : The mean wind speed. | |||
* {{PropertyData|WaveCelerity}} : The wave celerity corresponding to the modal frequency. | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | |||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Hasselmann Directional Spreading Function" | |||
featureGroup = "Directional Spreading Function" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not spreading: | |||
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n") | |||
return None | |||
spreading.ModalFrequency = '0.004 1/s' | |||
sim.MinDirection = '-90 deg' | |||
sim.MaxDirection = '90 deg' | |||
sim.NumberOfDirectionIncrements = 1024 | |||
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements | |||
sim.setActiveFeature(spreading) | |||
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s. | |||
frequency = 0.04 #hz | |||
# compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n") | |||
return None | |||
# let pick the first simulation point | |||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
# compute the spreading function vector for a frequency of 0.24 rad/s | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency) | |||
# show the results | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== Longuet Higgins Directional Spreading Function == | |||
The Longuet-Higgins directional spreading function is as follows: | |||
<math>D(\theta,\omega) = \frac{1}{2\sqrt{\pi}}\frac{\Gamma\left ( s+1\right )}{\Gamma\left ( s+1/2\right )}\mbox{cos}^{2s}\left ( \frac{\theta_w -\theta}{2} \right )</math> | |||
<math>s = 11.5\left ( \frac{g}{\omega_pU_{10}} \right )^{2.5}\left ( \frac{\omega}{\omega_p} \right )^{\mu}</math> | |||
=== Feature Dependency === | |||
The features required by this feature are summarized as follows: | |||
* A [[RPS_Feature_Group#Location_Distribution| simulation points feature]] | |||
* A [[RPS_Feature_Group#Frequency_Distribution| frequency discretization feature]] | |||
=== Properties === | |||
* {{PropertyData|PeakFrequency}}: The peak frequency. | |||
* {{PropertyData|TenMeterHeightMeanWindSpeed}} : The mean wind speed at ten meters above ground. | |||
* {{PropertyData|MainDirection}} : The main propagation direction of the wave. | |||
=== Scripting === | |||
The feature can be used from the python console as follows: | |||
{{Code|code= | |||
import SeaLab | |||
import SeaLabObjects | |||
import GeneralToolsGui | |||
import LabRPS | |||
from LabRPS import Vector as vec | |||
# Before you run this code, you should first have created a document with a SeaLab simulation with | |||
# active simulation points and frequency distribution | |||
def compute(): | |||
# get an existing SeaLab simulation called "Simulation" | |||
sim = SeaLab.getSimulation("Simulation") | |||
# check if the simulation does really exist | |||
if not sim: | |||
LabRPS.Console.PrintError("The simulation does not exist.\n") | |||
return None | |||
featureType = "Longuet-Higgins Directional Spreading Function" | |||
featureGroup = "Directional Spreading Function" | |||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | |||
# case you don't understand the next line) | |||
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | |||
if not spreading: | |||
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n") | |||
return None | |||
sim.MinDirection = '-90 deg' | |||
sim.MaxDirection = '90 deg' | |||
sim.NumberOfDirectionIncrements = 1024 | |||
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements | |||
sim.setActiveFeature(spreading) | |||
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s. | |||
frequency = 0.04 #hz | |||
# compute the simulation points coordinates | |||
simPoints = sim.computeLocationCoordinateMatrixP3() | |||
if not simPoints : | |||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n") | |||
return None | |||
# let pick the first simulation point | |||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | |||
# compute the spreading function vector for a frequency of 0.24 rad/s | |||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | |||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | |||
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency) | |||
# show the results | |||
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings) | |||
LabRPS.ActiveDocument.recompute() | |||
compute() | |||
}} | |||
[[#top| Back to the Top ]] | |||
== OrcaFlex Directional Spreading Function == | |||
The directional spreading spectrum used by OrcaFlex is: | |||
<math>D(\theta,\omega) | |||
= K(n)\ \cos^n(\theta-\theta_\mathrm{p}) \quad | |||
\text{ for } {-\tfrac\pi2} \leq \theta-\theta_\mathrm{p} \leq \tfrac\pi2 | |||
</math> | |||
where: | |||
<math> | |||
K(n) = \dfrac{\Gamma\left(\frac{n}{2}+1\right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}+\frac12\right)} | |||
</math> | |||
=== Feature Dependency === | === Feature Dependency === | ||
| Line 1,615: | Line 2,109: | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|PrincipalWaveDirection}}: The principal wave direction. | ||
* {{PropertyData| | * {{PropertyData|SpreadingExponent}} : The spreading exponent. | ||
=== Scripting === | === Scripting === | ||
| Line 1,641: | Line 2,135: | ||
return None | return None | ||
featureType = " | featureType = "OrcaFlex Directional Spreading Function" | ||
featureGroup = " | featureGroup = "Directional Spreading Function" | ||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | # case you don't understand the next line) | ||
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not spreading: | ||
LabRPS.Console.PrintError("Error on creating the | LabRPS.Console.PrintError("Error on creating the spreading function feature.\n") | ||
return None | return None | ||
sim. | sim.MinDirection = '-90 deg' | ||
sim. | sim.MaxDirection = '90 deg' | ||
sim. | sim.NumberOfDirectionIncrements = 1024 | ||
sim.setActiveFeature( | sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements | ||
sim.setActiveFeature(spreading) | |||
# For this example we shall compute the | # For this example we shall compute the spreading function for the frequency value of 0.25 rad/s. | ||
frequency = 0.04 #hz | |||
# compute the simulation points coordinates | # compute the simulation points coordinates | ||
| Line 1,665: | Line 2,160: | ||
if not simPoints : | if not simPoints : | ||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least | LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n") | ||
return None | return None | ||
# let pick the first simulation point | # let pick the first simulation point | ||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | ||
# compute the | # compute the spreading function vector for a frequency of 0.24 rad/s | ||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | # Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | ||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | # If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | ||
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency) | |||
# show the results | # show the results | ||
GeneralToolsGui.GeneralToolsPyTool.showArray(len( | GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings) | ||
LabRPS.ActiveDocument.recompute() | LabRPS.ActiveDocument.recompute() | ||
| Line 1,683: | Line 2,178: | ||
[[#top| Back to the Top ]] | [[#top| Back to the Top ]] | ||
== | == SWOP Directional Spreading Function == | ||
The SWOP(stereo wave observation project) directional spreading function is as follows: | |||
<math> | <math>D(\theta,\omega) = \frac{1}{\pi}\left \{ 1 + \left [ 0.5 +0.82\mbox{exp}\left [ \frac{\left ( \omega /\omega_0 \right )^4}{2} \right ] \right ] \mbox{cos}\left ( 2\theta \right )+ 0.32\mbox{exp}\left [ \frac{\left ( \omega /\omega_0 \right )^4}{2} \right ]\mbox{cos}\left ( 4\theta \right )\right \}</math> | ||
<math> | <math>\omega_0 = \frac{0.855\times g}{U_{10}}</math> | ||
=== Feature Dependency === | === Feature Dependency === | ||
The features required by this feature are summarized as follows: | The features required by this feature are summarized as follows: | ||
| Line 1,700: | Line 2,194: | ||
=== Properties === | === Properties === | ||
* {{PropertyData| | * {{PropertyData|TenMeterHeightMeanWindSpeed}} : The mean wind speed at ten meters above ground. | ||
=== Scripting === | === Scripting === | ||
| Line 1,728: | Line 2,219: | ||
return None | return None | ||
featureType = " | featureType = "SWOP Directional Spreading Function" | ||
featureGroup = " | featureGroup = "Directional Spreading Function" | ||
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | # create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in | ||
# case you don't understand the next line) | # case you don't understand the next line) | ||
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup) | |||
# check if the created feature is good | # check if the created feature is good | ||
if not | if not spreading: | ||
LabRPS.Console.PrintError("Error on creating the | LabRPS.Console.PrintError("Error on creating the spreading function feature.\n") | ||
return None | return None | ||
sim. | sim.MinDirection = '-90 deg' | ||
sim. | sim.MaxDirection = '90 deg' | ||
sim. | sim.NumberOfDirectionIncrements = 1024 | ||
sim.setActiveFeature( | sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements | ||
sim.setActiveFeature(spreading) | |||
# For this example we shall compute the | # For this example we shall compute the spreading function for the frequency value of 0.25 rad/s. | ||
frequency = 0.04 #hz | |||
# compute the simulation points coordinates | # compute the simulation points coordinates | ||
| Line 1,752: | Line 2,244: | ||
if not simPoints : | if not simPoints : | ||
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least | LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n") | ||
return None | return None | ||
# let pick the first simulation point | # let pick the first simulation point | ||
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3]) | ||
# compute the | # compute the spreading function vector for a frequency of 0.24 rad/s | ||
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | # Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization, | ||
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | # If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view. | ||
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency) | |||
# show the results | # show the results | ||
GeneralToolsGui.GeneralToolsPyTool.showArray(len( | GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings) | ||
LabRPS.ActiveDocument.recompute() | LabRPS.ActiveDocument.recompute() | ||
Latest revision as of 09:46, 9 February 2025
You can find the source code of this plugin on the following Github repository: Get the code here!. This plugin is one of the official plugins provided by LabRPS. It provides very useful features (tools) for the simulation of random sea elevations. Plugins are very easy to create in LabRPS, therefore, anyone can develop plugin for any random phenomenon in LabRPS. Go to this page to see how to create new plugin for LabRPS. You can get quick assistance from LabRPS community by sending your concern to the community forum.
Grid Points
This feature allows users to generate a set of grid points within a 3D spatial domain, ensuring that the points are evenly distributed in a plane parallel to one of the coordinate system planes (XY Plane, YZ Plane, XZ Plane).
Properties
- DataSpacing1: This is the points spacing along one of the axis forming the plane.
- DataSpacing2: This is the points spacing along the second axis.
- DataLength1: This is the length within points are distributed along one of the axis forming the plane.
- DataLength2: This is the length within points are distributed along the second axis.
- DataCenterPoint: This is the center of the grid around which the points are generated. It is a 3D point.
- DataNumberOfPoints: This is the resulting total number of points in the grid. This is a read only property for internal use. User cannot change its value directly.
Scripting
The following script shows how this feature can be created and used.
import SeaLab
import GeneralToolsGui
import SeaLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Grid Points"
featureGroup = "Location Distribution"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
unifSimPoints= SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not unifSimPoints:
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n")
return None
# set the plan the points grid is parallel to
unifSimPoints.LocationPlan= 'YZ Plane'
# let's set the center point of the distribution (x =0, y = 0, z = 0)
unifSimPoints.CenterPoint = vec(0,0,0)
# let's set the spacing1 (s1 = 10m)
unifSimPoints.Spacing1 = '10m'
# let's set the spacing2 (s2 = 10m)
unifSimPoints.Spacing2 = '10m'
# let's set the length1 (l1 = 200m)
unifSimPoints.Length1= '200m'
# let's set the length2 (l2 = 200m)
unifSimPoints.Length2= '200m'
# compute the simulation points coordinates. SeaLab will internally use the "unifSimPoints" feature.
simPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(simPoints)
# Example 3D points
x = arr[:,1]
y = arr[:,2]
z = arr[:,3]
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False)
# Create a figure
fig = plt.figure()
# Add 3D axes
ax = fig.add_subplot(111, projection='3d')
# Plot points
ax.scatter(x, y, z, color='blue')
# Hide all axes and labels
ax.set_axis_off()
# Set the title
ax.set_title('3D Plotting of Points')
# Show the plot
plt.show()
compute()
General Distribution
When the simulation points distribution is more general and does not follow any of the previous uniform distribution, this feature can be used. This feature allows users to input simulation points one by one using their coordinates based on the vector dialog shown below:
Properties
- DataLocations: This is a list holding the simulation points
Scripting
The following script shows how this feature can be created and used.
import SeaLab
import GeneralToolsGui
import SeaLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
def compute():
installResuslt = SeaLab.installPlugin("SeaLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create SeaLab simulation called "Simulation"
sim = SeaLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "General Distribution"
featureGroup = "Location Distribution"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
genSimPoints= SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not genSimPoints:
LabRPS.Console.PrintError("Error on creating the uniform points feature.\n")
return None
# create the simulation points by their coordinates
v1 = vec(0, 0, 35000)
v2 = vec(0, 0, 40000)
v3 = vec(0, 0, 140000)
# add the points to the locations
genSimPoints.Locations = [v1, v2, v3]
# compute the simulation points coordinates. SeaLab will internally use the "genSimPoints" feature
simPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(simPoints)
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, simPoints, False)
compute()
Import Simulation Points from File
When the simulation points are stored in a file, this feature can be used. The feature allows users to import simulation points coordinates from file. Note that, for now only tab separated text file is supported and the file is expected to have number of rows and number of columns which are number of simulation points and four, respectively.
File:SeaLab Tutorial001 Pic006 SeaLab Feat Locations 1.png
Properties
- DataFilePath: This is the path to the file.
Scripting
The following script shows how this feature can be created and used.
import SeaLab
import GeneralToolsGui
import SeaLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
def compute():
installResuslt = SeaLab.installPlugin("SeaLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create SeaLab simulation called "Simulation"
sim = SeaLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Import Simulation Points from File"
featureGroup = "Location Distribution"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
simPoints= SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not simPoints:
LabRPS.Console.PrintError("Error on creating the simulation points feature.\n")
return None
# set the direction of the distribution to be vertical
simPoints.FilePath = "D:/Points.txt"
# compute the simulation points coordinates. SeaLab will internally use the "simPoints" feature.
importedSimPoints = sim.computeLocationCoordinateMatrixP3()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(importedSimPoints )
# you can also show the result in a table, pass False as last argument to the function to ask
# LabRPS to only show the data without plotting them
GeneralToolsGui.GeneralToolsPyTool.showArray(sim.getSimulationData().numberOfSpatialPosition, 4, importedSimPoints, False)
compute()
Uniform Random Phases
In the simulation of random sea elevations, one common technique is to represent the random sea elevations as a sum of multiple sinusoidal components in the frequency domain. Each of these components is associated with a random phase, which determines the position of the sine wave relative to time. By assigning uniform random phases to each frequency component, the resulting time series will have random characteristics, while still adhering to the desired spectral properties, such as a specific power spectral density (PSD) or turbulence spectrum. The feature generate [math]\displaystyle{ n }[/math] sequences [math]\displaystyle{ (\phi_{1l}, \phi_{2l}, \phi_{3l},..., \phi_{nl}; l = 1, 2, 3, ..., N) }[/math] of independent random phase angles uniformly distributed over the interval [math]\displaystyle{ [0, 2\pi] }[/math] by default.
Properties
- DataMinimumValue: The minimum value that can be generated
- DataMaximumValue: The maximum value that can be generated
Scripting
The following script shows how this feature can be created and used.
import SeaLab
import SeaLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Uniform Random Phases"
featureGroup = "Randomness Provider"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
randomness = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not randomness:
LabRPS.Console.PrintError("Error on creating the randomness feature.\n")
# abord the computation
randomness.MinimumValue = 0
randomness.MaximumValue = 6.28
# generate random phase angle
randomnessMatrix = sim.generateRandomMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(randomnessMatrix)
Uniform Random Phases Import
When the simulation numbers are stored in a file, this feature can be used. The feature allows users to import random numbers from file. Note that, for now only tab separated text file is supported and the file is expected to have number of rows and number of columns which are number of frequency increments and number of simulation points, respectively.
Properties
- DataFilePath: This is the path to the file.
Scripting
The following script shows how this feature can be created and used.
import SeaLab
import SeaLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Uniform Random Phases Import"
featureGroup = "Randomness Provider"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
randomness = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not randomness:
LabRPS.Console.PrintError("Error on creating the randomness feature.\n")
# abord the computation
randomness.FilePath = "myfolderpath/myfile.txt"
# generate random phase angle
randomnessMatrix = sim.generateRandomMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(randomnessMatrix)
Single Index Frequency Discretization
This feature allows to discretize continuous frequency according to the following formula:
[math]\displaystyle{ \omega_{l} = l\Delta\omega; \quad l = 1, 2, 3, ..., N }[/math].
where:
- [math]\displaystyle{ \Delta\omega }[/math] is the frequency increment,
- [math]\displaystyle{ N }[/math] is the number of frequency increments,
Scripting
The following script shows how this feature can be created and used.
import SeaLab
import SeaLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Single Index Frequency Discretization"
featureGroup = "Frequency Distribution"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
frequency = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not frequency:
LabRPS.Console.PrintError("Error on creating the frequency feature.\n")
# abord the computation
# compute the freqency distribution
frequencyMatrix = sim.computeFrequenciesMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(frequencyMatrix)
Double Index Frequency Discretization
This feature allows to discretize continuous frequency according to the following formula:
[math]\displaystyle{ \omega_{ml} = (l-1)\Delta\omega + \frac{m}{n}\Delta\omega; \quad m = 1, 2, 3, ..., n; \quad l = 1, 2, 3, ..., N }[/math].
where:
- [math]\displaystyle{ \Delta\omega }[/math] is the frequency increment,
- [math]\displaystyle{ n }[/math] is the number of simulation points,
- [math]\displaystyle{ N }[/math] is the number of frequency increments,
Scripting
The following script shows how this feature can be created and used.
import SeaLab
import SeaLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Double Index Frequency Discretization"
featureGroup = "Frequency Distribution"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
frequency = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not frequency:
LabRPS.Console.PrintError("Error on creating the frequency feature.\n")
# abord the computation
# compute the freqency distribution
frequencyMatrix = sim.computeFrequenciesMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(frequencyMatrix)
Zerva Frequency Discretization
This feature allow to discretize continuous frequency according to the following formula:
[math]\displaystyle{ \omega_{l} = (1+\frac{l}{2})\Delta\omega;\quad l = 1, 2, 3, ..., N }[/math],
where:
- [math]\displaystyle{ \Delta\omega }[/math] is the frequency increment,
- [math]\displaystyle{ N }[/math] is the number of frequency increments,
Scripting
The following script shows how this feature can be created and used.
import SeaLab
import SeaLabObjects
from LabRPS import Vector as vec
import numpy
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
# abord the computation
featureType = "Zerva Frequency Discretization"
featureGroup = "Frequency Distribution"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
frequency = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not frequency:
LabRPS.Console.PrintError("Error on creating the frequency feature.\n")
# abord the computation
# compute the freqency distribution
frequencyMatrix = sim.computeFrequenciesMatrixFP()
# now you can convert the coordinate matrix to numpy array and use it for any other purposes
arr = numpy.asarray(frequencyMatrix)
Cholesky Decomposition
This feature performs the Cholesky decomposition of a positive Hermitian power spectrum matrix and returns the lower triangular matrix (L) of the decomposition. The Cholesky decomposition is a numerical method used to decompose a positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. Specifically, for a matrix A, the decomposition is given by:
[math]\displaystyle{ \mathbf{A} = \mathbf{L L}^{*}, }[/math]
[math]\displaystyle{ L_{j,j} = \sqrt{ A_{j,j} - \sum_{k=1}^{j-1} L_{j,k}^*L_{j,k} }, }[/math]
[math]\displaystyle{ L_{i,j} = \frac{1}{L_{j,j}} \left( A_{i,j} - \sum_{k=1}^{j-1} L_{j,k}^* L_{i,k} \right) \quad \text{for } i\gt j. }[/math]
where [math]\displaystyle{ L }[/math] is a lower triangular matrix with real and positive diagonal entries, and [math]\displaystyle{ L^* }[/math] denotes the conjugate transpose of [math]\displaystyle{ L }[/math].
The feature is optimized for performance and can handle large matrices efficiently using [math]\displaystyle{ O(n^3) }[/math] computational complexity in the worst case. It checks if the input matrix is indeed positive-definite and Hermitian before performing the decomposition and raises an error if the matrix does not meet these conditions. The feature belong to the PSD Decomposition Method feature group.
Feature Dependency
The features required by this feature are summarized as follows:
Scripting
The feature can be used from the python console as follows:
import SeaLab
import GeneralToolsGui
import SeaLabObjects
from LabRPS import Vector as vec
import LabRPS
import numpy
def compute():
installResuslt = SeaLab.installPlugin("SeaLabPlugin")
doc = LabRPS.ActiveDocument
if not doc:
doc = LabRPS.newDocument()
# create SeaLab simulation called "Simulation"
sim = SeaLabObjects.makeSimulation(doc, "Simulation")
# check if the simulation sucessfully created
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Cholesky Decomposition"
featureGroup = "Spectrum Decomposition Method"
# create the feature
decomposedPSD = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not decomposedPSD :
LabRPS.Console.PrintError("Error on creating the spectrum decomposition method.\n")
return None
# get the active simulation points feature and compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# use a vector to represent a simulation point based on its coordinates
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
v2 = vec(simPoints[1][1], simPoints[1][2], simPoints[1][3])
v3 = vec(simPoints[2][1], simPoints[2][2], simPoints[2][3])
# This feature is used to decompose power spectrum matrices which may vary in time. Let's assume that
# the active power spectrun density function in this example is stationary. Meanning it is not varying in time.
#Then, we use time instant of 0 second.
time = 0.0
# compute the decomposed cross spectrum between points 1 and 3, at time instant of 0 second and for all frequency
# increments. Note that when the following code is run, SeaLab will try to identify the active frequency distribution,
# the active power spectrum feature, the active coherence function feature and others. If SeaLab fails to find any
# of these dependency features, the computation will fails and specific error messages will be sent to the report view.
psd13 = sim.computeDecomposedCrossSpectrumVectorF(v1, v3, time)
# psd13 can be converted to numpy vector and be used for some other purposes.
arr = numpy.asarray(psd13)
compute()
Pierson Moskowitz Spectrum 1964
Various idealized spectra are used to answer the question in oceanography and ocean engineering. Perhaps the simplest is that proposed by Pierson and Moskowitz 1964. They assumed that if the wind blew steadily for a long time over a large area, the waves would come into equilibrium with the wind. This is the concept of a fully developed sea (a sea produced by winds blowing steadily over hundreds of miles for several days).Here, a long time is roughly ten-thousand wave periods, and a "large area" is roughly five-thousand wave-lengths on a side. (source):
[math]\displaystyle{ S(\omega) = \frac{5}{16}H^2_s\omega^4_p\omega^{-5}\mbox{exp}\left [ -\frac{5}{4}\left ( \frac{\omega}{\omega_p} \right )^{-4} \right ] }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: The significant wave height.
- DataPeakPeriod: The peak period.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Pierson Moskowitz Spectrum (1964)"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
Jonswap Spectrum 1974
Hasselmann et al. 1973, after analyzing data collected during the Joint North Sea Wave Observation Project JONSWAP, found that the wave spectrum is never fully developed. It continues to develop through non-linear, wave-wave interactions even for very long times and distances. Hence an extra and somewhat artificial factor was added to the Pierson-Moskowitz spectrum in order to improve the fit to their measurements. The JONSWAP spectrum is thus a Pierson-Moskowitz spectrum multiplied by an extra peak enhancement factor [math]\displaystyle{ \gamma ^r }[/math] (source):
[math]\displaystyle{ S(\omega) = \frac{5}{16}A_{\gamma}H^2_s\omega^4_p\omega^{-5}\mbox{exp}\left [ -\frac{5}{4}\left ( \frac{\omega}{\omega_p} \right )^{-4} \right ]\gamma^r }[/math]
where:
[math]\displaystyle{ A_{\gamma} = 1 - 0.287 \times ln\left ( \gamma \right ) \quad \mbox{is a normalizing factor} }[/math]
[math]\displaystyle{ r = \mbox{exp}\left [ -\frac{1}{2}\left ( \frac{\omega-\omega_p}{\sigma\omega_p} \right )^{2} \right ] }[/math]
[math]\displaystyle{ \sigma =
\begin{cases}
\sigma_1, & \mbox{for } \omega \le \omega_p \\
\\
\sigma_2, & \mbox{for } \omega \gt \omega_p
\end{cases}
}[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: The significant wave height.
- DataPeakPeriod: The peak period.
- DataAutoGamma: Whether to automatically compute gamma or not.
- DataAutoSigma: Whether to automatically compute sigma or not.
- DataGamma: The value of shape parameter gamma.
- DataSigma1: The width of spectral peak sigma 1.
- DataSigma2: The width of spectral peak sigam 2.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Jonswap Spectrum (1974)"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
Gaussian Swell Spectrum
The Gaussian swell spectrum is based on the normal (or Gaussian) probability density function and is defined as (source):
[math]\displaystyle{ S(\omega) = \left ( \frac{H_c}{4} \right )^2\frac{1}{\sigma\sqrt{2\pi}}\mbox{exp}\left [ -\frac{\left ( \omega -\omega_p \right )^2}{2\sigma^2} \right ] }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: The significant wave height.
- DataPeakFrequency: The peak frequency.
- DataSigma: The width of spectral peak sigma.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Gaussian Swell Spectrum"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
Ochi Hubble Spectrum
The Ochi-Hubble spectrum allows double-peaked spectra to be set up, enabling you to represent sea states that include both a remotely generated swell and a local wind generated sea. See the Ochi-Hubble paper for full details. (source):
[math]\displaystyle{ S(\omega) = \sum_{j=1}^2 \left\{ \frac{\left(\frac{4\lambda_j+1}{4}\right)^{\lambda_j} \omega_{\mathrm{m}_j}^{4\lambda_j}H_{\mathrm{s}_j}^2}{4\Gamma(\lambda_j)} \right\} \omega^{-(4\lambda_j+1)} \exp\left\{ -\left(\frac{4\lambda_j+1}{4}\right) \left(\frac{\omega}{\omega_{\mathrm{m}_j}}\right)^{-4} \right\} }[/math]
where:
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataPeakShape1: The peak shape of the first peak.
- DataPeakShape2: The peak shape of the second peak.
- DataPeakFrequency1: The peak frequency of the first peak.
- DataPeakFrequency2: The peak frequency of the second peak.
- DataSignificantWaveHeight1: The significant wave height of the first peak.
- DataSignificantWaveHeight2: The significant wave height of the second peak.
- DataAutoPara: Whether to automatically compute the six previous parameter.
- DataSignificantWaveHeight: The significant wave height used the calculate those six parameters in case of automatic parameters calculation .
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Ochi-Hubble spectrum"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
Torsethaugen Spectrum
The Torsethaugen spectrum is another two-peaked spectrum, more suited to North Sea application than Ochi-Hubble. The spectrum is defined by two user input parameters, [math]\displaystyle{ H_s }[/math] and [math]\displaystyle{ T_p (= 1/f_m) }[/math]. In order to define the spectrum we must first define a number of other terms (source):
[math]\displaystyle{ \begin{array}{lcl} a_1 = 0.5 \\ a_2 = 0.3 \\ a_3 = 6 \\ a_{10} = 0.7 \\ a_{20} = 0.6 \\ b_1 = 2\ \textrm{s} \\ G_0 = 3.26 \\ k_g = 35 \\ k_1 = 0.0016 \\ k_2 = 0.286 \\ k_3 = \frac{k_2}{k_1^{1/3}} \\ k_f = k_3 g^{-1/2} \\ F_e = 370,000\ \textrm{m} \\ a_f = k_f F_e^{1/6} \\ T_{pf} = a_f H_s^{1/3} \\ a_e = 2\ \textrm{sm}^{-1/2} \\ T_l = a_e H_s^{1/2} \\ T_u = 25\ \textrm{s} \\ \epsilon_l = \frac{T_{pf} - T_p}{T_{pf} - T_l} \\ \epsilon_u = \frac{T_p - T_{pf}}{T_u - T_{pf}} \\ \end{array} }[/math]
Note: [math]\displaystyle{ \mbox{If }\epsilon_l \lt 0 \mbox{ then } \epsilon_l \mbox{ is set to 0. If } \epsilon_l \gt 1 \mbox{ then } \epsilon_l \mbox{ is set to 1. Likewise for } \epsilon_u.\\ }[/math]
For wind dominated sea, [math]\displaystyle{ T_p \le T_{pf} }[/math], we define:
[math]\displaystyle{ \begin{array}{lcl} R_w = (1 - a_{10}) \exp\{-(\epsilon_l/a_1)^2\} + a_{10} \\ H_1 = R_w H_s \\ T_{p1} = T_p \\ s_p = \frac{2\pi}{g}\frac{H_1}{T_{p1}^2} \\ \gamma = k_g s_p^{6/7} \\ H_2 = (1 - R_w^2)^{1/2} H_s \\ T_{p2} = T_{pf} + b_1 \\ \end{array} }[/math]
For swell dominated sea, [math]\displaystyle{ T_p \gt T_{pf} }[/math], we define:
[math]\displaystyle{ \begin{array}{lcl} R_s = (1 - a_{20}) \exp(-(\epsilon_u/a_2)^2) + a_{20} \\ H_1 = R_s H_s \\ T_{p1} = T_p \\ s_f = \frac{2\pi}{g}\frac{H_s}{T_{pf}^2} \\ \gamma_f = k_g s_f^{6/7} \\ \gamma = \gamma_f (1 + a_3 \epsilon_u) \\ H_2 = (1 - R_s^2)^{1/2} H_s \\ T_{p2} = a_f H_2^{1/3} \\ \end{array} }[/math]
Note: If [math]\displaystyle{ \gamma \lt 1 }[/math] then [math]\displaystyle{ \gamma }[/math] is set to 1.
These two branches of the formulation define [math]\displaystyle{ H_1, H_2, T_{p1}, T_{p2} }[/math] and [math]\displaystyle{ \gamma }[/math] which are then used to define the spectrum as
[math]\displaystyle{ S(f) = \sum_{j=1}^2 E_j S_{jn}(f_{jn}) }[/math]
where:
[math]\displaystyle{ \begin{array}{lcl} j = 1\ \textrm{is the primary sea system} \\ j = 2\ \textrm{is the secondary sea system} \\ f_{1n} = f T_{p1} \\ f_{2n} = f T_{p2} \\ \sigma = \begin{cases} 0.07 \quad \mbox{for } f_{1n} \le 1 \\ 0.09 \quad \mbox{for } f_{1n} \gt 1 \\ \end{cases} \\ E_1 = (1/16) H_1^2 T_{p1} \\ E_2 = (1/16) H_2^2 T_{p2} \\ A_\gamma = \frac{1 + 1.1 \log_e(\gamma)^{1.19}}{\gamma} \\ S_{1n}(f_{1n}) = G_0 A_\gamma f_{1n}^{-4} \exp(-f_{1n}^{-4}) \gamma^{\exp\{-(1/2\sigma^2) (f_{1n} - 1)^2\}} \\ S_{2n}(f_{2n}) = G_0 f_{2n}^{-4} \exp(-f_{2n}^{-4}) \\ \end{array} }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: The significant wave height.
- DataPeakPeriod: The peak period.
- DataAutoGamma: Whether to automatically compute gamma or not.
- DataAutoSigma: Whether to automatically compute sigma or not.
- DataGamma: The value of shape parameter gamma.
- DataSigma1: The width of spectral peak sigma 1.
- DataSigma2: The width of spectral peak sigam 2.
- DataDoublePeaks: Whether double peaks or not.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Torsethaugen Spectrum"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
Bretschneider Spectrum
The Bretschneider Spectrum is a two-parameter spectral model based on the assumption that the waves are narrow-banded with the wave characteristics following the Rayleigh distribution:
[math]\displaystyle{ S(\omega) = C_1\times H^2_s\left ( \frac{\omega^4_0}{\omega^5} \right )\mbox{exp}\left [ C_2\left ( \frac{\omega_0}{\omega} \right )^2 \right ] }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: The significant wave height.
- DataSignificantWavePeriod: The significant wave period defined as the average period of the significant waves.
- DataConstant1: A constant (0.2107 by default).
- DataConstant2: A constant (-0.8429 by default).
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Bretschneider Spectrum"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
ISSC Spectrum
The International Ship Structures Congress (1964) suggested slight modification of the Bretschneider spectrum given as:
[math]\displaystyle{ S(\omega) = C_1\times H^2_s\left ( \frac{\omega^4_0}{\omega^5} \right )\mbox{exp}\left [ C_2\left ( \frac{\omega_0}{\omega} \right )^2 \right ] }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: The significant wave height.
- DataSignificantWavePeriod: The significant wave period defined as the average period of the significant waves.
- DataConstant1: A constant (0.3123 by default).
- DataConstant2: A constant (-1.2489 by default).
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "ISSC Spectrum"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
ITTC Spectrum
The Pierson Moskowitz spectrum was modified in the International Towing Tank Conference (1966, 1969,1972) given as:
[math]\displaystyle{ S(\omega) = \alpha g^2\omega^{-5}\mbox{exp}\left ( -\frac{4\alpha g^2\omega^{-4}}{H^2_s} \right ) }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: The significant wave height.
- DataPhillipsConstant:The Phillips Constant (0.0081 by default).
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "ITTC Spectrum"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
Scott Spectrum
The Pierson Moskowitz spectrum was modified in the International Towing Tank Conference (1966, 1969,1972) given as:
[math]\displaystyle{ S(\omega) = 0.214 H^2_s\mbox{exp}\left [ -\frac{1}{0.065}\left ( \frac{\omega-\omega_p}{ \omega-\omega_p +0.26} \right )^{1/2} \right ], \quad \mbox{for } -0.26\lt \omega-\omega_p \lt 1.65 \mbox{ and } 0 \mbox{ elsewhere.} }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: the significant wave height.
- DataPeakFrequency the peak frequency of the spectrum.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Scott Spectrum"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '0.04 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
WEN Spectrum
WEN spectrum is the wave spectrum of China offshore. It can describe the different stages of wind wave growth and adapt to different water depths:
[math]\displaystyle{ S(\omega) = \frac{m_0p}{\omega_w}\mbox{exp}\left \{ -95\left [ ln\frac{p \left ( 5.813− 5.137\eta \right )}{\left ( 6.77− 1.088p+0.013p^2 \right )\left ( 1.307− 1.426\eta \right )} \right ]\left ( \frac{\omega}{\omega_0} - 1\right )^{12/5} \right \}, \quad \mbox{for } 0 \le \omega \le 1.15\omega_w }[/math]
[math]\displaystyle{ S(\omega) = \frac{m_0}{\omega_w} \frac{\left ( 6.77− 1.088p+0.013p^2 \right )\left ( 1.307− 1.426\eta \right )}{ 5.813− 5.137\eta} \left ( \frac{1.15\omega_w}{\omega} \right )^m, \quad \mbox{for } \omega \ge 1.15\omega_w }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataSignificantWaveHeight: the significant wave height.
- DataSignificantWavePeriod significant wave period defined as the average period of the significant waves.
- DataDepthParameter: The depth parameter taken between 0 and 0.5.
- DataTenMetersHeightMeanWindSpeed the mean wind speed at 10 meters above ground.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "WEN Spectrum"
featureGroup = "Frequency Spectrum"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spectrum = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spectrum:
LabRPS.Console.PrintError("Error on creating the spectrum function feature.\n")
return None
sim.MaxFrequency = '4 1/s'
sim.NumberOfFrequency = 1024
sim.FrequencyIncrement = sim.MaxFrequency/sim.NumberOfFrequency
sim.setActiveFeature(spectrum)
# For this example we shall compute the cross spectrum matrix at time instant of 0 second and for the frequency value of 0.25 rad/s.
time = 0.0
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least 3 simulation points.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spectrum vector at time instant of 0 second
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spectrums = sim.computeAutoFrequencySpectrumVectorF(v1, time)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spectrums), len(spectrums[0]), spectrums)
LabRPS.ActiveDocument.recompute()
compute()
Borgman Directional Spreading Function
The Borgman directional spreading function is based on a circular normal distribution of Mobarek (1965) and Fan (1968):
[math]\displaystyle{ D(\theta) = \frac{1}{2I_0\left ( \theta_p \right )}\mbox{exp}\left [ a\mbox{cos}\left ( \theta - \theta_p \right ) \right ] }[/math]
where:
[math]\displaystyle{ I_0\left ( \theta_p \right ) }[/math] is the Bessel function of the second kind and zeroth order.
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataAngleOfPropagationOfPredominantWaveEnergy: The angle of propagation of predominant wave energy..
- DataPositiveConstant : A positive constant.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Borgman Directional Spreading Function"
featureGroup = "Directional Spreading Function"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spreading:
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n")
return None
sim.MinDirection = '-90 deg'
sim.MaxDirection = '90 deg'
sim.NumberOfDirectionIncrements = 1024
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements
sim.setActiveFeature(spreading)
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s.
frequency = 0.04 #hz
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spreading function vector for a frequency of 0.24 rad/s
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings)
LabRPS.ActiveDocument.recompute()
compute()
Cos2s Directional Spreading Function
The Cos2s directional spreading function is based on the cosine function with a spreading parameter which does not vary with frequency:
[math]\displaystyle{ D(\theta) = \frac{\Gamma^2\left ( s+1\right )}{\Gamma\left ( 2s+1\right )}\mbox{cos}^{2s}\left ( \frac{\theta -\theta_0}{2} \right ) }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataPrincipalWaveDirection: The angle defining the principal direction in which the wave is propagating.
- DataSpreadingExponent :The spreading exponent.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Cos2s Directional Spreading Function"
featureGroup = "Directional Spreading Function"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spreading:
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n")
return None
sim.MinDirection = '-90 deg'
sim.MaxDirection = '90 deg'
sim.NumberOfDirectionIncrements = 1024
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements
sim.setActiveFeature(spreading)
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s.
frequency = 0.04 #hz
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spreading function vector for a frequency of 0.24 rad/s
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings)
LabRPS.ActiveDocument.recompute()
compute()
Cosine Squared Directional Spreading Function
The cosine squared directional spreading function assumes that spreading is proportional to [math]\displaystyle{ (cos 0)^2 }[/math]. It does not vary with frequency:
[math]\displaystyle{ D(\theta) = \left ( \frac{2}{\pi} \right )\mbox{cos}^{2}\left ( \theta \right ) }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Cosine Squared Directional Spreading Function"
featureGroup = "Directional Spreading Function"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spreading:
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n")
return None
sim.MinDirection = '-90 deg'
sim.MaxDirection = '90 deg'
sim.NumberOfDirectionIncrements = 1024
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements
sim.setActiveFeature(spreading)
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s.
frequency = 0.04 #hz
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spreading function vector for a frequency of 0.24 rad/s
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings)
LabRPS.ActiveDocument.recompute()
compute()
Mitsuyasu Directional Spreading Function
Mitsuyasu et al. (1975) propose the following directional spreading function:
[math]\displaystyle{ D(\theta, \omega) = \frac{2^{2s-1}}{\pi}\frac{\Gamma^2\left ( s+1\right )}{\Gamma\left ( 2s+1\right )}\left | \mbox{cos}\left ( \frac{\theta}{2} \right )\right |^{2s} }[/math]
where:
[math]\displaystyle{ s = \begin{cases} s_m\left ( \frac{\omega}{\omega_m} \right )^5, & \mbox{for } \omega \le \omega_m \\ \\ s_m\left ( \frac{\omega}{\omega_m} \right )^{-2.5}, & \mbox{for } \omega \gt \omega_m \end{cases} }[/math]
[math]\displaystyle{ s_m = 11.5\left ( \frac{\omega_mU}{g} \right )^{-2.5} }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataModalFrequency: The modal frequency.
- DataTenMeterHeightmeanWindSpeed : The mean wind speed at 10 meters above aground.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Mitsuyasu Directional Spreading Function"
featureGroup = "Directional Spreading Function"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spreading:
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n")
return None
spreading.ModalFrequency = '0.004 1/s'
sim.MinDirection = '-90 deg'
sim.MaxDirection = '90 deg'
sim.NumberOfDirectionIncrements = 1024
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements
sim.setActiveFeature(spreading)
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s.
frequency = 0.004 #hz
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spreading function vector for a frequency of 0.24 rad/s
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings)
LabRPS.ActiveDocument.recompute()
compute()
Hasselmann Directional Spreading Function
From analysis of measured data, Hasselmann et al. (1980) propose the following directional spreading function:
[math]\displaystyle{ D(\theta, \omega) = \frac{2^{2s-1}}{\pi}\frac{\Gamma^2\left ( s+1\right )}{\Gamma\left ( 2s+1\right )}\left | \mbox{cos}\left ( \frac{\theta}{2} \right )\right |^{2s} }[/math]
where:
[math]\displaystyle{ s = \begin{cases} 6.97\left ( \frac{\omega}{\omega_m} \right )^{4.06}, & \mbox{for } \omega \le 1.05\omega_m \\ \\ 9.77\left ( \frac{\omega}{\omega_m} \right )^{\mu}, & \mbox{for } \omega \gt 1.05\omega_m \end{cases} }[/math]
[math]\displaystyle{ s_m = -2.33-1.45\left ( \frac{\omega_mU}{g} -1.17\right ) }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataModalFrequency: The modal frequency.
- DataMeanWindSpeed : The mean wind speed.
- DataWaveCelerity : The wave celerity corresponding to the modal frequency.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Hasselmann Directional Spreading Function"
featureGroup = "Directional Spreading Function"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spreading:
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n")
return None
spreading.ModalFrequency = '0.004 1/s'
sim.MinDirection = '-90 deg'
sim.MaxDirection = '90 deg'
sim.NumberOfDirectionIncrements = 1024
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements
sim.setActiveFeature(spreading)
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s.
frequency = 0.04 #hz
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spreading function vector for a frequency of 0.24 rad/s
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings)
LabRPS.ActiveDocument.recompute()
compute()
Longuet Higgins Directional Spreading Function
The Longuet-Higgins directional spreading function is as follows:
[math]\displaystyle{ D(\theta,\omega) = \frac{1}{2\sqrt{\pi}}\frac{\Gamma\left ( s+1\right )}{\Gamma\left ( s+1/2\right )}\mbox{cos}^{2s}\left ( \frac{\theta_w -\theta}{2} \right ) }[/math]
[math]\displaystyle{ s = 11.5\left ( \frac{g}{\omega_pU_{10}} \right )^{2.5}\left ( \frac{\omega}{\omega_p} \right )^{\mu} }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataPeakFrequency: The peak frequency.
- DataTenMeterHeightMeanWindSpeed : The mean wind speed at ten meters above ground.
- DataMainDirection : The main propagation direction of the wave.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "Longuet-Higgins Directional Spreading Function"
featureGroup = "Directional Spreading Function"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spreading:
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n")
return None
sim.MinDirection = '-90 deg'
sim.MaxDirection = '90 deg'
sim.NumberOfDirectionIncrements = 1024
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements
sim.setActiveFeature(spreading)
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s.
frequency = 0.04 #hz
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spreading function vector for a frequency of 0.24 rad/s
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings)
LabRPS.ActiveDocument.recompute()
compute()
OrcaFlex Directional Spreading Function
The directional spreading spectrum used by OrcaFlex is:
[math]\displaystyle{ D(\theta,\omega)
= K(n)\ \cos^n(\theta-\theta_\mathrm{p}) \quad
\text{ for } {-\tfrac\pi2} \leq \theta-\theta_\mathrm{p} \leq \tfrac\pi2
}[/math]
where:
[math]\displaystyle{ K(n) = \dfrac{\Gamma\left(\frac{n}{2}+1\right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}+\frac12\right)} }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataPrincipalWaveDirection: The principal wave direction.
- DataSpreadingExponent : The spreading exponent.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "OrcaFlex Directional Spreading Function"
featureGroup = "Directional Spreading Function"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spreading:
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n")
return None
sim.MinDirection = '-90 deg'
sim.MaxDirection = '90 deg'
sim.NumberOfDirectionIncrements = 1024
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements
sim.setActiveFeature(spreading)
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s.
frequency = 0.04 #hz
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spreading function vector for a frequency of 0.24 rad/s
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings)
LabRPS.ActiveDocument.recompute()
compute()
SWOP Directional Spreading Function
The SWOP(stereo wave observation project) directional spreading function is as follows:
[math]\displaystyle{ D(\theta,\omega) = \frac{1}{\pi}\left \{ 1 + \left [ 0.5 +0.82\mbox{exp}\left [ \frac{\left ( \omega /\omega_0 \right )^4}{2} \right ] \right ] \mbox{cos}\left ( 2\theta \right )+ 0.32\mbox{exp}\left [ \frac{\left ( \omega /\omega_0 \right )^4}{2} \right ]\mbox{cos}\left ( 4\theta \right )\right \} }[/math]
[math]\displaystyle{ \omega_0 = \frac{0.855\times g}{U_{10}} }[/math]
Feature Dependency
The features required by this feature are summarized as follows:
Properties
- DataTenMeterHeightMeanWindSpeed : The mean wind speed at ten meters above ground.
Scripting
The feature can be used from the python console as follows:
import SeaLab
import SeaLabObjects
import GeneralToolsGui
import LabRPS
from LabRPS import Vector as vec
# Before you run this code, you should first have created a document with a SeaLab simulation with
# active simulation points and frequency distribution
def compute():
# get an existing SeaLab simulation called "Simulation"
sim = SeaLab.getSimulation("Simulation")
# check if the simulation does really exist
if not sim:
LabRPS.Console.PrintError("The simulation does not exist.\n")
return None
featureType = "SWOP Directional Spreading Function"
featureGroup = "Directional Spreading Function"
# create the feature and add it to the existing simulation (you may refer to the SeaLab Workbench page in
# case you don't understand the next line)
spreading = SeaLabObjects.makeFeature("MyNewFeature", sim.Name, featureType, featureGroup)
# check if the created feature is good
if not spreading:
LabRPS.Console.PrintError("Error on creating the spreading function feature.\n")
return None
sim.MinDirection = '-90 deg'
sim.MaxDirection = '90 deg'
sim.NumberOfDirectionIncrements = 1024
sim.DirectionIncrement = (sim.MaxDirection-sim.MinDirection)/sim.NumberOfDirectionIncrements
sim.setActiveFeature(spreading)
# For this example we shall compute the spreading function for the frequency value of 0.25 rad/s.
frequency = 0.04 #hz
# compute the simulation points coordinates
simPoints = sim.computeLocationCoordinateMatrixP3()
if not simPoints :
LabRPS.Console.PrintError("Make sure you have an active location disttribution in the simulation with at least one simulation point.\n")
return None
# let pick the first simulation point
v1 = vec(simPoints[0][1], simPoints[0][2], simPoints[0][3])
# compute the spreading function vector for a frequency of 0.24 rad/s
# Note that when the following code is run, SeaLab will try to identify the active locations distribution, the active frequency discretization,
# If SeaLab fails to find these dependency features, the computation will fails and specific error messages will be sent to the report view.
spreadings = sim.computeDirectionalSpreadingFunctionVectorD(v1, frequency)
# show the results
GeneralToolsGui.GeneralToolsPyTool.showArray(len(spreadings), len(spreadings[0]), spreadings)
LabRPS.ActiveDocument.recompute()
compute()